1. 基本概念
图的基本概念中我们需要掌握的有这么几个概念:无向图、有向图、带权图;顶点(vertex);边(edge);度(degree)、出度、入度。下面我们就从无向图开始讲解这几个概念。
如图所示是一个无向图,图中的元素(A、B、C、D、E、F)被称为顶点(vertex),顶点可以与任意顶点建立连接关系,这种关系叫做边(edge),无向图中边是没有方向的。顶点相连接的边的条数就被称为度(degree),图中顶点 A 的度就是 3 。
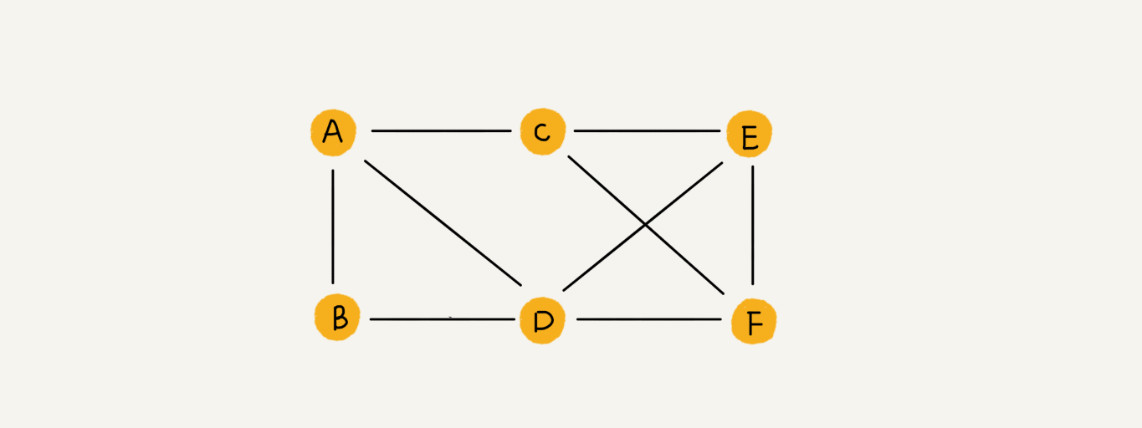
还有一种图,图中的边是有方向的,如图所示,则将这种图称为有向图。度这种概念在有向图中又被扩展为入度和出度。顶点的入度是指有多少条边指向这个顶点;顶点的出度指有多少条边以这个顶点为起点。
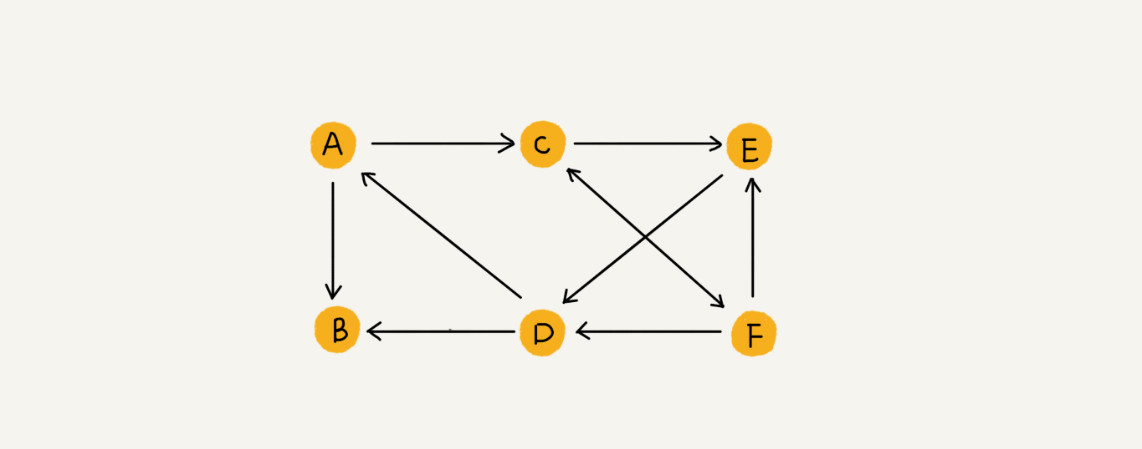
上述的边都没有权重,假如我们要拿一个图来存储地图数据的话,图中的边还需要表示距离,那么这个图就变成了带权图(weighted graph)。在带权图中,每条边都有一个权重,这个权重可以表示距离。
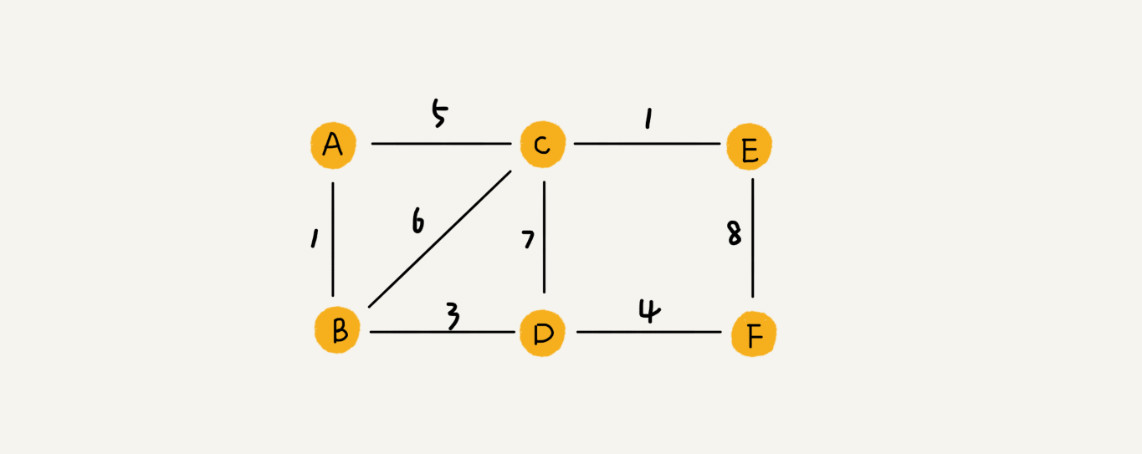
综上来看的,图的类型主要是根据边的类型来决定的。
2. 图的存储
图的基本概念不多,那么在计算机中我们该如何存储图这种数据结构呢?主要有两种方式来存储图,一种是邻接矩阵的方法,另一种是邻接表的方式。
2.1. 邻接矩阵
邻接矩阵是图最直观的一种存储方式,底层依赖于二维数组。
- 对于无向图来说,如果顶点 i 和顶点 j 之间有边那么则将
A[i][j]和A[j][i]标记为 1 - 对于有向图来说,如果顶点 i 有一条边指向顶点 j,但是顶点 j 没有一条边指向顶点 i,那么则将
A[i][j]标记为 1,但是A[j][i]不用标记为 1。 - 对于带权图来说,只是从存储 1 变成存储具体的权重。
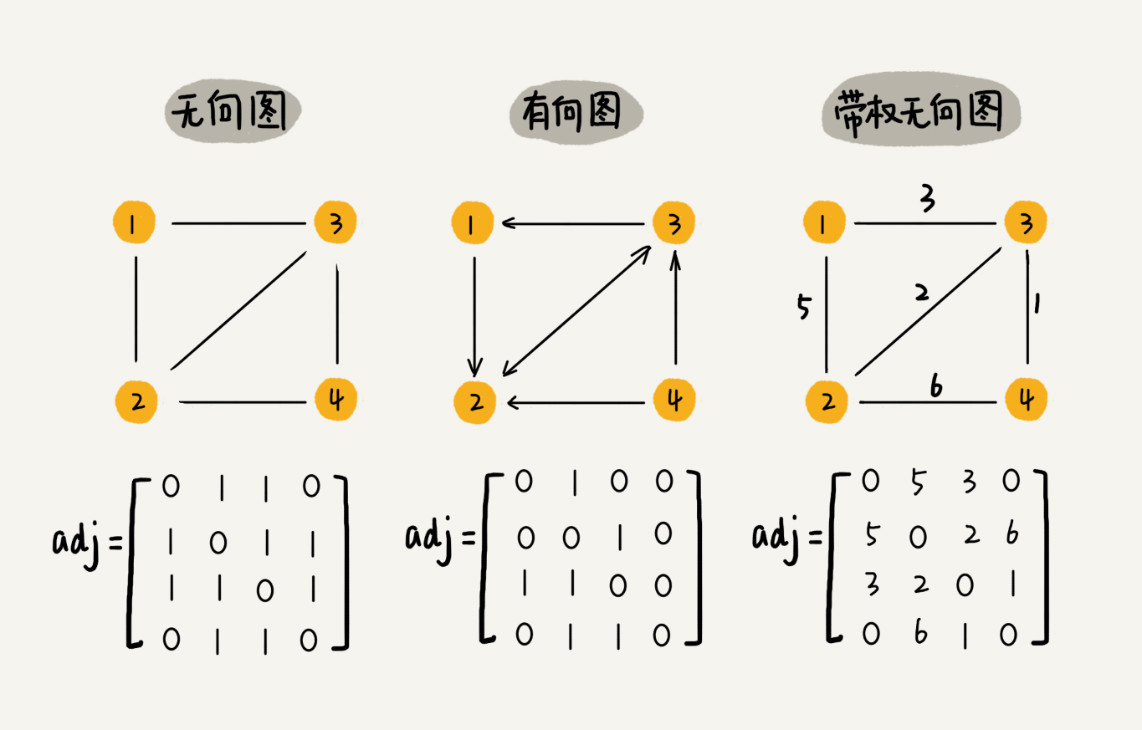
-
邻接矩阵的缺点是在表示一个图时通常很浪费存储空间。
对于无向图来说,它是一个对称矩阵,即
A[i][j]等于 1 的话,那么A[j][i]也等于 1。那么实际上只要存储一半就可以了。另外,假如存储的是稀疏图,也就是顶点很多,但是每个顶点的边不多的一种图。那么使用邻接矩阵存储将更浪费存储空间,因为很多位置的值都是 0,这些 0 其实都是没有用的。
-
邻接矩阵的优点就是存储方式简单、直观,而且获取两个顶点的关系时非常高效。另外,使用邻接矩阵时,在计算上也很方便。因为很多图的运算实际上可以转换为矩阵的运算,比如求最短路径问题时会提到一个 Floyd-Warshall 算法,这个算法会利用到矩阵循环相乘若干次的结果。
2.2. 邻接表
图的另一种存储方法,是使用邻接表(Adjacency List)。如图所示,有向图中的每个顶点对应一个链表,该链表中存储的是该顶点指向的顶点。对于无向图来说是类似的,每个节点对应的链表中存储的是该节点所相连的顶点。
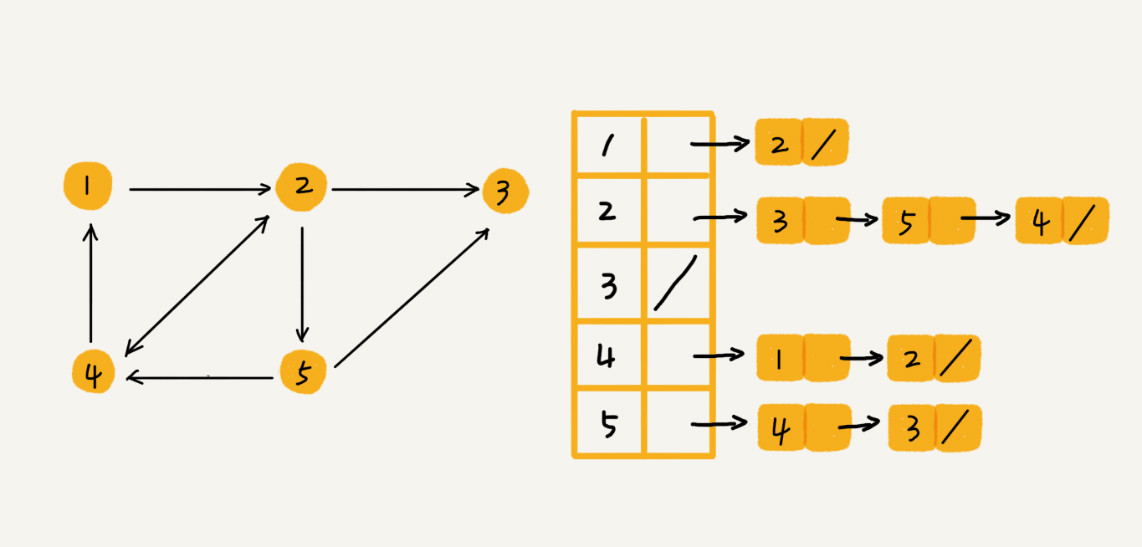
- 邻接表相比邻接矩阵的一个优点就是节省空间,但是使用起来比较耗时间(时间换空间的设计思想)。在使用邻接矩阵判断无向图中 i 和 j 之间是否存在一条边,那么只需要判断
A[i][j]是否为 1,而在邻接表中判断无向图中 i 和 j 之间是否存在一条边,那么需要判断 i 这个顶点对应的链表中是否存在 j。而且链表的方式对于缓存来说不太友好。所以,综上来说在邻接表中查询两个顶点的关系没有邻接矩阵那么高效了。 - 但是,为了让查询变得更加高效。我们可以参考散列表中提到的那样,将链表换成平衡二叉查找树(比如红黑树),或者其他动态数据结构,比如跳表、散列表,有序动态数组(结合二分查找)等。
逆邻接表
邻接表中存储的是这个顶点指向的顶点,那么逆邻接表中存储的是指向这个顶点的顶点。比如要想查看 4 这个顶点指向了哪些节点就可以使用邻接表。但是想要查看有哪些节点指向了 4 这个顶点,那么就需要逆邻接表了。
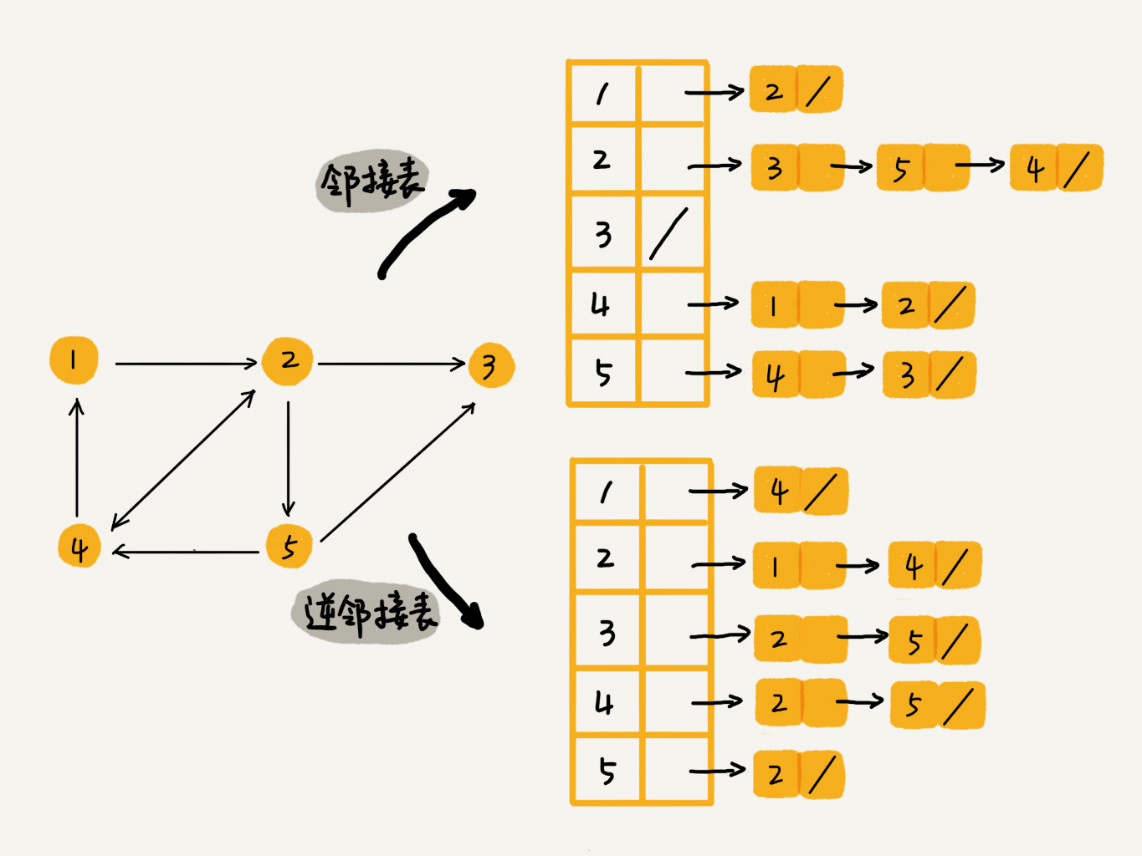
2.3. 总结
综上来说,邻接矩阵的缺点是比较浪费空间,但是优点是查询效率高,还方便矩阵运算。邻接表的优点是节省存储空间,但是不方便查找(查找效率肯定没邻接矩阵高)。对于此,我们可以将链表替换成查询效率较高的动态数据结构,比如平衡二叉树(红黑树)、跳表、散列表等。
3. 图的搜索
图上的搜索算法,最直接的理解就是,在图中找出从一个顶点出发,到另一个顶点的路径。具体方法有很多,比如有最简单、最“暴力”的深度优先、广度优先搜索,还有 A*、IDA* 等启发式搜索算法。深度优先、广度优先搜索即可以用在有向图,也可以用在无向图上。下面的实现以无向图和邻接表的存储方式为例。
3.1. 广度优先搜索(Breath-First-Search)
广度优先搜索,简称 BFS。这种搜索方法是一层层的向外搜索,先从起点开始,然后再搜索离起点最近的顶点;之后再从离起点最近的顶点出发搜索离这些顶点最近的顶点。整个过程示意图如图所示,跟二叉树的层次遍历是一样的。
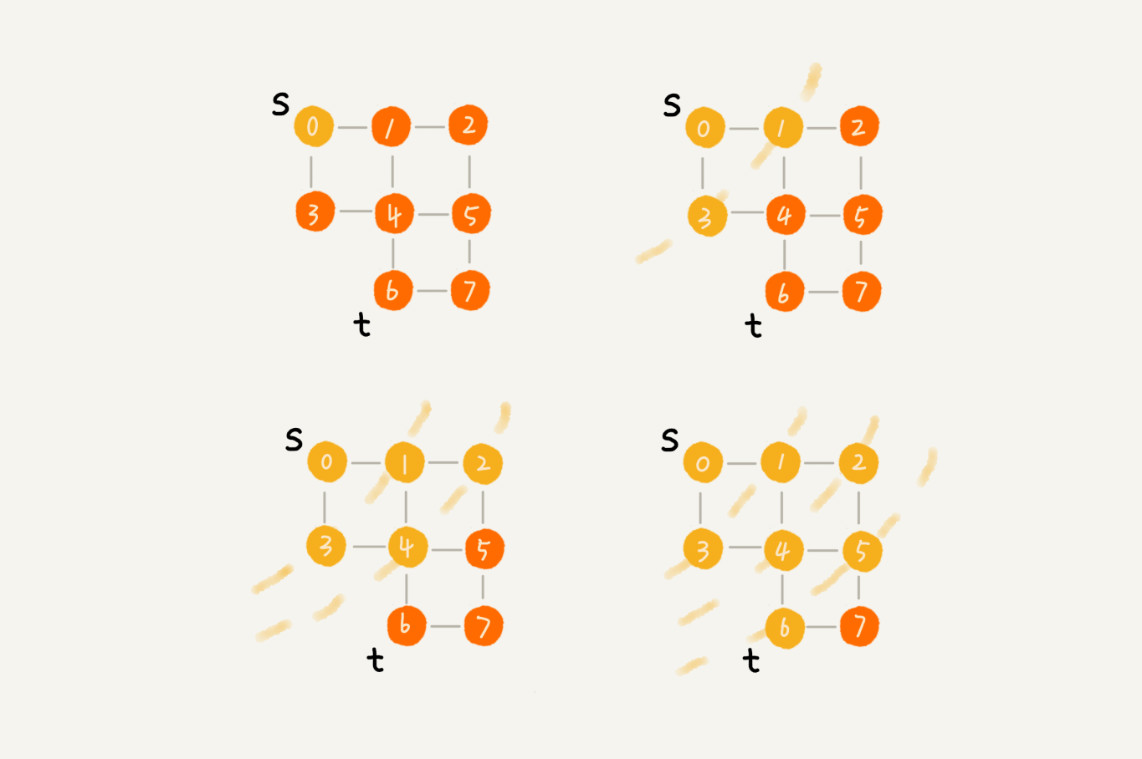
相应的代码实现,如下代码所示。from 表示起点,to 表示终点。和层次遍历一样,广度优先搜索使用了队列这种数据结构。队列主要用来存储那些已经被访问,但是相邻的顶点还没有被访问的顶点。为什么使用队列这种数据结构呢?从应用场景出发,因为广度优先搜索方法是逐层访问的。也就是先访问 k 层的顶点,访问之后再去访问 k+1 层的顶点。但是,在访问第 k 层顶点的时候需要将 k+1 层的顶点也保存下来,而且 k+1 层顶点是在第 k 层顶点之后被访问并从队列中退出,也就相当于 “后来后出”。
但是,相比层次遍历又多一些内容,主要多出的是 visited 和 paths 这两个数组,visited 数组主要是用来存储顶点是否已经被访问过了,因为图相比树更为复杂,有些顶点会有多个相邻顶点。为了避免顶点被重复访问,所以借用了一个数组。
paths 数组主要用来记录从 from 到 to 的广度搜索路径,但是每个数组元素(数组下标即顶点编号)只存储该顶点前面的那个顶点,比如 paths[3] 存储 2,则表示是先访问到 2 ,然后从 2 再访问到 3。这样的存储方式是逆向的,为了正向地输出搜索路径,可以使用递归的方式,递归的时候将输出放置到递归之后。因为只有等前面的顶点递归完成之后,再输出本顶点,才是正向的路径。
public void bfsSearch(int from, int to) {
if (this.v == 0 || from == to) {
return;
}
boolean[] visited = new boolean[this.v];
int[] paths = new int[this.v]; // 记录路径,记录该节点前面的节点是哪个
for (int i = 0; i < this.v; i++) {
visited[i] = false;
paths[i] = -1;
}
Queue<Integer> queue = new LinkedList<>();
queue.offer(from);
visited[from] = true;
while (!queue.isEmpty()) {
int w = queue.poll();
for (Integer i : this.adj[w]) {
if (!visited[i]) {
queue.offer(i);
visited[i] = true;
paths[i] = w;
if (i == to) {
printPath(paths, to);
break;
}
}
}
}
}
另外,需要明白的是在没有权重的图中,广度优先搜索的结果就是最短路径。这个是因为广度优先搜索的方式中,每次都是取最近的节点,那么当到达终点时,其实所需次数是最少的。
时间复杂度
广度优先搜索的时间复杂度最坏是遍历整个图,那么此时每个顶点都会被遍历到,每条边也会被访问一次。那么,假设边数为 E,顶点数为 V,此时时间复杂度为 O(V+E)(针对邻接表来说)。
空间复杂度
广度优先搜索时,空间复杂度主要来自于队列、visited 数组、paths 数组。这些数组的大小最大为 V,因为空间复杂度是 O(V)。
3.2. 深度优先搜索(Depth-First-Search)
深度优先搜索,简称 DFS。怎么直观的理解呢?就是你从一个顶点出发,假如这个顶点有未被访问过的顶点则访问它,然后一个一个这么套下去。当一个顶点的相邻顶点都被访问过了,那么则退回上一个顶点,然后看一下上一个顶点是否有未被访问过的邻接顶点,有的话则访问它,然后一层一层下去。如果也都被访问过了,那么则再退。一个典型的生活中的例子就是走迷宫,先一条道走到“黑”,然后看不到出口了,上一个分叉口再换条道。
如图所示,这是在图上采用深度优先搜索之后的样子,实现表示搜索方向,虚线表示回退。
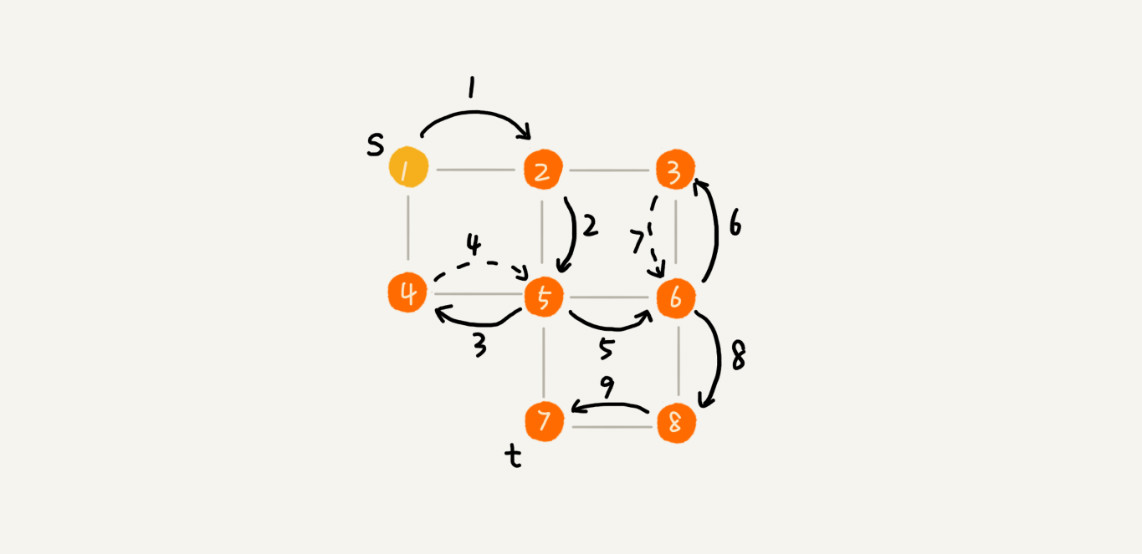
深度优先搜索采用的思想是回溯思想,这种思想比较适合使用递归。我们使用递归的方式实现一下 DFS。相比 BFS,DFS 多了一个 find 变量,这个变量用于判断是否有找到顶点的。如果在没有遍历到一个顶点的最后一个邻接顶点之前就找到了终点,那么接下去的邻接顶点就可以不用遍历了,直接返回即可。
public void dfsSearch(int from, int to) {
if (this.v == 0 || from == to) {
return;
}
boolean[] visited = new boolean[this.v];
int[] paths = new int[this.v];
for (int i = 0; i < this.v; i++) {
visited[i] = false;
paths[i] = -1;
}
visited[from] = true;
reDFSS(from, to, visited, paths);
if (this.FIND_DFS == true) {
printPath(paths, to);
}
}
public void reDFSS(int from, int to, boolean[] visited, int[] paths) {
if (from == to) {
this.FIND_DFS = true;
return;
}
for (Integer i : this.adj[from]) {
if (this.FIND_DFS) {
return;
}
if (!visited[i]) {
visited[i] = true;
paths[i] = from;
reDFSS(i, to, visited, paths);
}
}
}
除了使用递归的方式实现之外,还可以将递归的方式转化成栈和循环结合的方式。在图的遍历这小节内容,你会看到非递归的方式。
深度优先搜索找到的并不是最短路径。
时间复杂度
采用同样的方法,从顶点和边的被访问次数出发,每条边最多被两次访问(一次遍历,一次回退),每个顶点被访问一次,那么时间复杂度是 O(V+E)(针对邻接表来说)。
空间复杂度
同样的,深度优先搜索的方式的空间复杂度主要来源栈、visited 数组和 paths 数组,栈的长度不可能超过顶点的个数,因此空间复杂度还是 O(V)。
3.3. 总结
- 广度和深度相比其他高级搜索算法(比如 A*算法)更简单粗暴,没有什么优化,也被称为暴力搜索算法。这两种算法适用于图不大的情况。
- 深度优先搜索主要借助了栈的方式,这个栈可以是函数调用栈也可以是栈这种数据结构(因为递归也可以转化为非递归的方式)。广度优先搜索主要使用队列。
- 图和树的比较,图的 DFS 类似于树的先序遍历;BFS 类似于树的层次遍历。
- 在没有权重的图中,BFS 搜索的路径结果就是最短路径;DFS 搜索的结果却不一定,因为 DFS 会“绕来绕去”,而 BFS 很直接每次都是最近的。
- 在求图的时间复杂度时,常用的方法是从顶点和边被遍历的次数出发。
4. 图的遍历
与图的搜索算法有点不同的是,图的遍历是指将图中的所有点都遍历一次。常见的遍历方法有深度优先遍历和广度优先遍历。这两种遍历方法的思想还是一样的,简单来说就是图的搜索方法就是加了一个节点判断,如果找到相应的节点就停止搜索。下面直接给出相应的代码,不再赘述。
4.1. 广度优先遍历
public void bfsTraversal() {
if (this.v == 0) {
return;
}
boolean[] visited = new boolean[this.v];
for (int i = 0; i < this.v; i++) {
visited[i] = false;
}
Queue<Integer> queue = new LinkedList<>();
queue.offer(0);
visited[0] = true;
while (!queue.isEmpty()) {
int w = queue.poll();
System.out.print(w + "\t");
for (Integer i : this.adj[w]) {
if (visited[i] == false) {
queue.offer(i);
visited[i] = true;
}
}
}
}
4.2. 深度优先遍历
// 递归的方式
public void dfsTraversal() {
if (this.v == 0) {
return;
}
boolean[] visited = new boolean[this.v];
for (int i = 0; i < this.v; i++) {
visited[i] = false;
}
for (int i = 0; i < this.v; i++) {
if (!visited[i]) {
reDFST(i, visited);
}
}
}
public void reDFST(int f, boolean[] visited) {
visited[f] = true;
System.out.print(f + "\t");
for (Integer i : this.adj[f]) {
if(!visited[i]) {
reDFST(i, visited);
}
}
}
// 非递归的方式,使用了栈
public void dfsTraversalStack() {
if (this.v == 0) {
return;
}
boolean[] visited = new boolean[this.v];
for (int i = 0; i < this.v; i++) {
visited[i] = false;
}
Stack<Integer> stack = new Stack<>();
stack.push(0);
visited[0] = true;
System.out.print(0 + "\t");
while (!stack.isEmpty()) {
int w = stack.peek();
int flag = 0;
for (Integer i : this.adj[w]) {
if (!visited[i]) {
stack.push(i);
visited[i] = true;
System.out.print(i + "\t");
flag = 1;
break;
}
}
if (flag == 0) {
stack.pop();
}
}
}
巨人的肩膀
- 极客时间-《数据结构与算法》-王争老师

