数据结构和算法 | 二分查找大家都会，那么二分查找的变体呢？【6】

1. 前言

大家好，我是多选参数的程序锅，一个正在”捣鼓“操作系统、学数据结构和算法以及 Java 的硬核菜鸡。

二分查找大家估计都会，但是二分查找的变体大家会吗？我相信你是会的，我这个菜鸡就是不会了，所以在学习二分查找变体的时候，我感觉发现了新大陆。

为了整个知识的相对完整，下面还是从最基本的二分查找开始讲解，之后讲解二分查找的变体，这个变体在刷 Leetcode 的有些题目的时候也会用到。最后对二分查找这种算法进行总结。

本篇相关的代码都可以从 https://github.com/DawnGuoDev/algorithm 获取，另外，该仓库除了包含了基础的数据结构和算法实现之外，还会有数据结构和算法的笔记、LeetCode 刷题记录（多种解法、Java 实现） 、一些优质书籍整理。

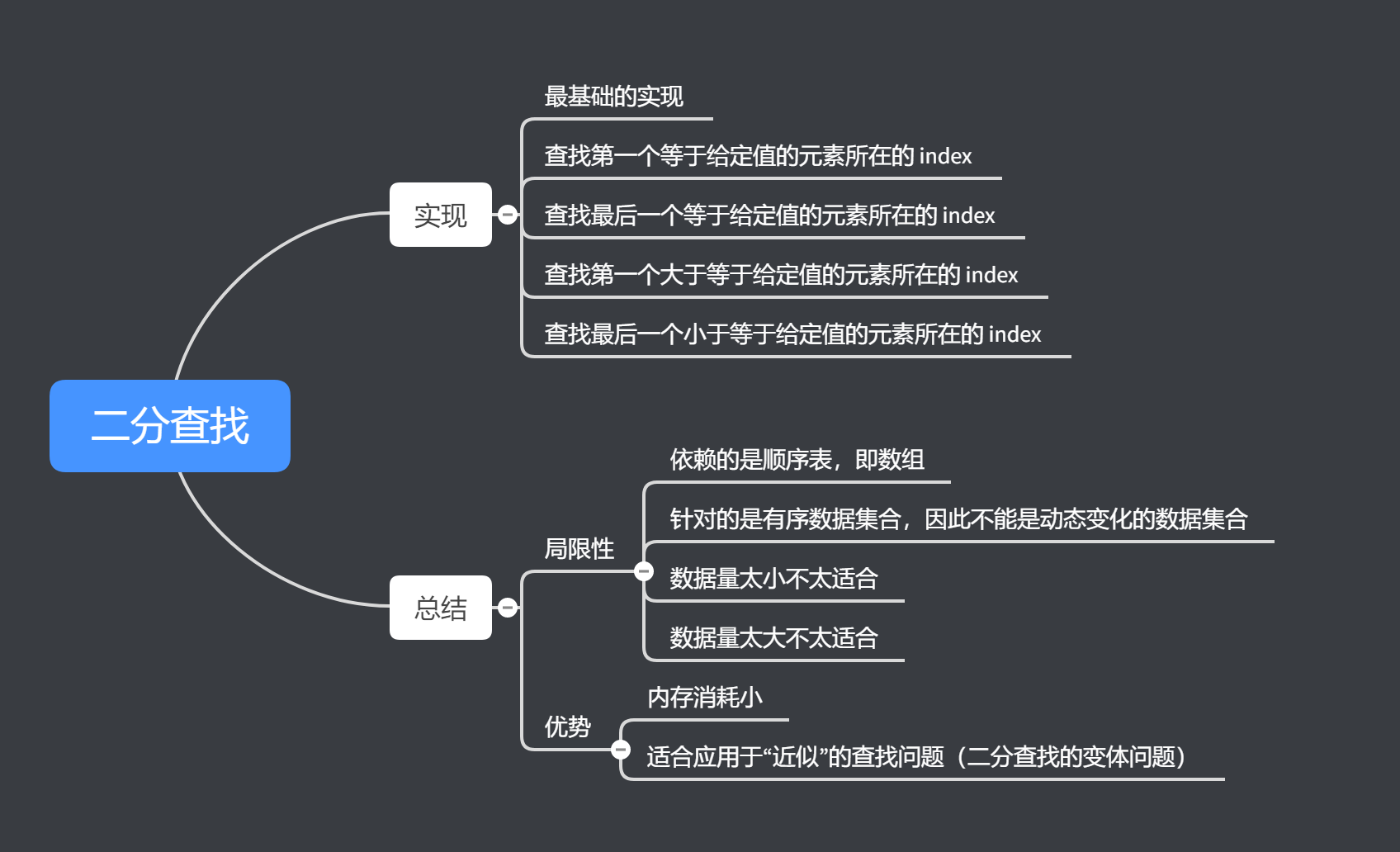
2. 二分查找及其变体

二分查找针对的是一个有序的数据集合（必须是有序），查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半（或者说剔除了另一半数据），直到找到要查找的元素，或者区间被缩小为 0。

由于经过一次查找，会剔除一半数据而剩下另一半数据，因此经过 k 次查找之后，剩下的数据个数为 $n*\frac{1}{2^{k}$，整个二分查找当剩下一个元素的时候停止，**因此需要经过 $log_2}n$ 次查找，时间复杂度也就是 $O(logn)$。**

2.1. 最基础的实现

这边先讲解不存在重复元素的有序数组中，查找值等于给定值的元素的情况（PS：全文的讲解都以数据是从小到大排列为前提）。

2.1.1. 非递归的方式

public int bsearch(int[] array, int len, int value) {
    int low = 0;
    int high = len - 1;

    while (low <= high) {
        int mid = low + ((high - low) >> 1);
        if (array[mid] == value) {
            return mid;
        } else if (array[mid] < value) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }

    return -1;
}

在实现非递归算法时，需要注意以下几个关键点：

• 循环的条件是 low <= high，而不是 low < high。因为可能 low 和 high 重合的时候正是需要查询的值，比如 1,2,3 那么假如我要查询 3 这个值的位置时，是在 low 等于 high 的时候才查询到的。
• mid = (low+high)/2 这种写法不太严谨，因为 low 和 high 比较大的时候，可能就会溢出。所以，改进的方法是 mid = low +(high-low)/2。当然为了追求性能的极致，那么可以将这里的除以 2 改为移位操作。因为移位操作比除法运算来说，计算机处理前者会更快。最终为 mid = low + ((high-low)>>1)。需要注意的是，考虑到移位操作和加法的优先级，这边的括号必须要这样。
• low 和 high 值的更新，这边一定要记得 +1 和 -1，否则的话可能会进入死循环。假如没有+1 或者 -1 的操作，那么 1,2,3 我要查询的是 3 这个值，第一步 low=0， high=2；第二步 low=1，high=2；第三步还是 low=1，high=2。

2.1.2. 递归的方式

public int bsearchInternally(int[] array, int low, int high, int value) {
    if (low > high) {
        return -1;
    }

    int mid = low + ((high -  low) >> 1);
    if (array[mid] == value) {
        return mid;
    } else if (array[mid] < value) {
        return bsearchInternally(array, mid + 1, high, value);
    } else {
        return bsearchInternally(array, low, mid - 1, value);
    }
}

这边的注意点与非递归的注意点是一一对应的，递归方式注意的是循环的条件，非递归方式注意的则是递归终止的条件，这边需要 low>high 而不是 low >= high，理由是一样的，自己举例看一下。其他两个注意事项是一样的。

回忆一下递归方式编写代码的技巧：1.是先写出递归式；2.确定终止条件；3.翻译成代码。

2.2. 查找第一个等于给定值的元素所在的 index

接下去讲解二分查找的变体，主要考虑几种典型的情况。首先，将不存在重复元素的有序数组进行一般化，即有序数组集合中存在重复的数据。那么我们该如何找到第一个等于给定值的数据的 index 呢？

假如按照最简单的方式来实现查找的话（即上述的实现），那么得到的结果将不一定正确。比如下面这个存在重复数据的有序数组集合。假设要查找的数据是 8 ，那么先拿 8 和第 4 个数据 6 进行比较，发现 8 比 6 大，于是在下标 5-9 之间寻找。结果发现第 7 个数据 8 正好是要查找的数据，然后将 index 7 返回，但是实际上第一个 8 的 index 应该是 5。

1  3  4  5  6  8  8  8  11  18

因此，对于这个变形问题，我们需要改造一下之前的代码。改造之后的代码如下所示：

public int bsearchFirstEqual(int[] array, int len, int value) {
    int low = 0;
    int high = len - 1;

    while (low <= high) {
        int mid = low + ((high - low) >> 1);
        if (array[mid] < value) {
            low = mid + 1;
        } else if (array[mid] > value) {
            high = mid - 1;
        } else {
            if (mid == 0 || array[mid - 1] != value) {
                return mid;
            }
            high = mid - 1;
        }
    }
    return -1;
}

这边稍微解析一下代码。a[mid]跟要查找的 value 的大小关系有三种情况：大于、小于、等于。对于 a[mid] >value的情况，说明等于情况位于 low-mid 之间，所以 high = mid-1。对于 a[mid]<value 的情况，说明等于情况位于 mid-high 之间，所以 low = mid+1。对于 a[mid]=value的情况，我们需要确保 mid 这个 index 是不是第一个等于 value 的 index。因此，先判断 mid 等不等于 0，假如等于的话，那么肯定是第一个了；之后判断 mid-1 位置的元素等不等于 value，如果不等于 value，那么说明 mid 是第一个等于 value 的 index。假如 mid-1 位置的元素等于 value，那么说明第一个等于 value 在 mid 之前，所以 high=mid-1。

2.3. 查找最后一个等于给定值的元素所在的 index

前面是查找第一个值等于给定值的元素，现在将问题稍微改一下，查找最后一个值等于定值的元素的 index。相应的实现代码其实和前面的类似。

public int bsearchLastEqual(int[] array, int len, int value) {
    int low = 0;
    int high = len - 1;

    while (low <= high) {
        int mid = low + ((high - low) >> 1);

        if (array[mid] < value) {
            low = mid + 1;
        } else if (array[mid] > value) {
            high = mid - 1;
        } else {
            if (mid == len -1 || array[mid + 1] != value) {
                return mid;
            }
            low = mid + 1;
        }
    }

    return -1;
}

这里我们就不分析了，分析思路跟上面的那种情况类似。

2.4. 查找第一个大于等于给定值的元素所在的 index

看完查找值相等的情况之后，接下去我们查找值不相等的情况。在有序数组中（可含重复元素），查找第一个大于等于给定值的元素的 index。比如针对序列：3、4、6、7、10，查找第一个大于等于 5 的元素，那就是 6 ，index 是 2。

public int bsearchFirstMore(int[] array, int len, int value) {
    int low = 0; 
    int high = len - 1;

    while (low <= high) {
        int mid = low + ((high - low) >> 1);

        if (array[mid] < value) {
            low = mid + 1;
        } else {
            if (mid == 0 || array[mid - 1] < value) {
                return mid;
            }
            high = mid - 1;                
        }
    }

    return -1;
}

如果 mid 位置所在的元素小于 value，那么第一个大于等于 value 的值的 index 是在 [mid+1, high] 之间，所以 low=mid+1。如果 mid 位置所在的元素已经大于 value，那么需要判断 mid 是不是第一个大于等于 value 的 index。假如 mid == 0 ，那么肯定是第一个了；或者 mid 前面的那个元素小于 value，那么 mid 也是第一个大于等于 value 的 index。如果两个条件都不满足，那么第一个大于等于 value 的 index，是在 [low, mid-1] 之间，因此将 high 进行更新。

2.5. 查找最后一个小于等于给定值的元素所在的 index

现在将问题变成查找最后一个小于等于给定值的元素的 index。比如针对序列：3、5、6、8、9、10，最后一个小于等于给定值 7 的元素是 6， index 是 2 。代码的实现思路与上述情况相似。

public int bsearchLastLess(int[] array, int len, int value) {
    int low = 0;
    int high = len - 1;

    while (low <= high) {
        int mid = low + ((high - low) >> 1);

        if (array[mid] > value) {
            high = mid - 1;
        } else {
            if (mid == len - 1 || array[mid + 1] > value) {
                return mid;
            }
            low = mid + 1;
        }
    }

    return -1;
}

这里我们就不分析了，分析思路跟上面的那种情况类似。

3. 总结

3.1. 二分查找的局限性

虽然二分查找的时间复杂度是 O(logn)，查找效率极高，但是二分查找却不是完美的，这种查找方法存在一些局限性。

• 二分查找依赖的是顺序表结构，简单点说就是数组。

  二分查找能否依赖其他数据结构呢？比如链表。答案是不可以的，主要原因是二分查找算法是按照下标随机访问元素的，比如我们访问 mid 这个位置的数据就是通过下标随机访问的，这个时间复杂度是 O(1)。假如使用链表方式的话，需要遍历到 mid 这个位置，那么时间复杂度为 O(n)。所以，如果数据使用链表存储，二分查找的时间复杂度会变得高。

• 二分查找针对的是有序数据，在动态变化的数据集合中不适用

  二分查找的时候要求查找的数据序列必须是有序的。如果数据不是有序的，那么需要先排序才能查找。在使用时间复杂度为 O(nlogn)的排序算法的情况下。如果一组静态的数据，没有频繁地插入、删除等操作，二分查找还是可以接受的。因为我们可以进行一次排序，多次二分查找。这样排序的成本就会被均摊。但是，如果我们的数据集合有频繁的插入和删除操作的话，要想二分查找。那么每次插入、删除之后都需要进行排序，从而反正数据序列的有序。这种情况下，维护有序的时间成本时很高的。

  综上，二分查找只能用于插入、删除操作不频繁，一次排序多次查找的情况。针对动态变化的数据集合，二分查找将不再适合。

• 数据量太小不适合二分查找

  要处理的数据量很小的话，完全没有必要用二分查找，顺序遍历就可以了。比如要在 10 个有序的数组中查找一个元素，不管使用顺序遍历还是二分查找，查找速度都查不多。但是这种情况下有个例外，就是如果比较操作非常耗时的话，那么也请用二分查找，因为虽然两者次数差不多，但是这种情况下我们是需要尽可能减少比较的次数。显然，二分查找的次数还会更少一点。

• 数据量太大也不适合二分查找

  二分查找的底层需要依赖数组这种数据结构，而数组这种数据结构要求内存空间的连续。假如数据量太大，比如有 1GB 大小的数据，如果使用数组来存储，那么就需要 1GB 的连续内存空间。所以当要查找的数据集合特别大的时候二分查找也会不太适合。

3.2. 二分查找的优势

• 二分查找在内存使用上更节省

  虽然大部分情况下，用二分查找的方式可以解决的问题，散列表、二叉树都可以解决。但是，不管是散列表还是二叉树都需要额外的内存空间。而二分查找依赖的是数组，除了数据本身之外，不需要存储额外的其他信息。所以当二分查找需要 100MB 内存的情况下，散列表或二叉树需要的内存空间会更大（不止 100MB）。显然，在这三种方式中二分查找是最省内存空间的。

• 二分查找更适合用在“近似”查找问题。

  在这类问题上，二分查找的优势更加明显，就比如这几种变体。而查找“等于给定值”的问题，更适合散列表或二叉树。这种变体的二分查找算法比较难写，尤其是细节上如果处理不好容易产生BUG，这些出错的细节有：终止条件、区间上下界更新方法、返回值选择。

巨人的肩膀

1. 极客时间专栏，王争老师的《数据结构与算法之美》

附 Github

整个系列的代码可查看 github 仓库 https://github.com/DawnGuoDev/algos ，这个仓库将主要包含常用数据结构及其基本操作的手写实现（Java），也会包含常用算法思想经典例题的实现（Java）。在接下来一年内，这个仓库将会保持更新状态，在此之间学到的关于数据结构和算法的知识或者实现也都会往里面 commit，所以赶紧来 star 哦。