数据结构和算法 | 这次用近万字的讲解带你干掉堆！【3】

1. 前言

大家好，我是多选参数的程序锅，一个正在捣鼓操作系统、学数据结构和算法以及 Java 的失业人员。最近忙着搞论文，还有刷刷 LeetCode 上的题，推文的事被耽误了一下，但是并没有忘记要发推文，虽迟但到吧。

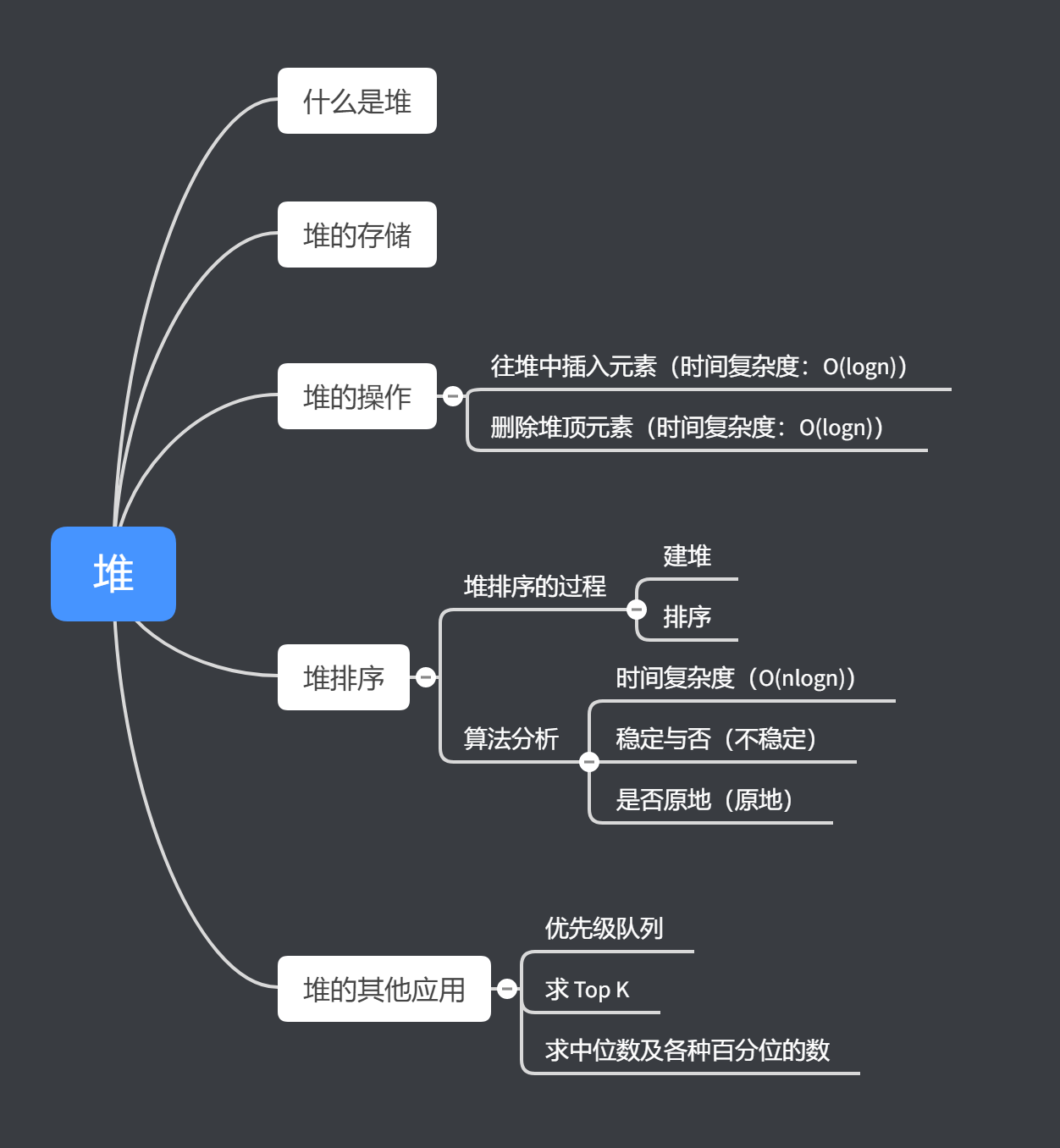
整篇文章的主要知识提纲如图所示，本篇相关的代码都可以从 https://github.com/DawnGuoDev/algorithm 获取，另外，该仓库除了包含了基础的数据结构和算法实现之外，还会有数据结构和算法的笔记、LeetCode 刷题记录（多种解法、Java 实现）、一些优质书籍整理。

2. 基本概念

堆是一种特殊的树。只要满足以下两个条件就是一个堆。

堆是一个完全二叉树。既然是完全二叉树，那么使用数组存储的方式将会很方便。
堆中的每个节点的值都必须大于等于（或小于等于）其子节点的值。对于大于等于子节点的堆又被称为“大顶堆”；小于等于子节点的堆又被称为“小顶堆”。

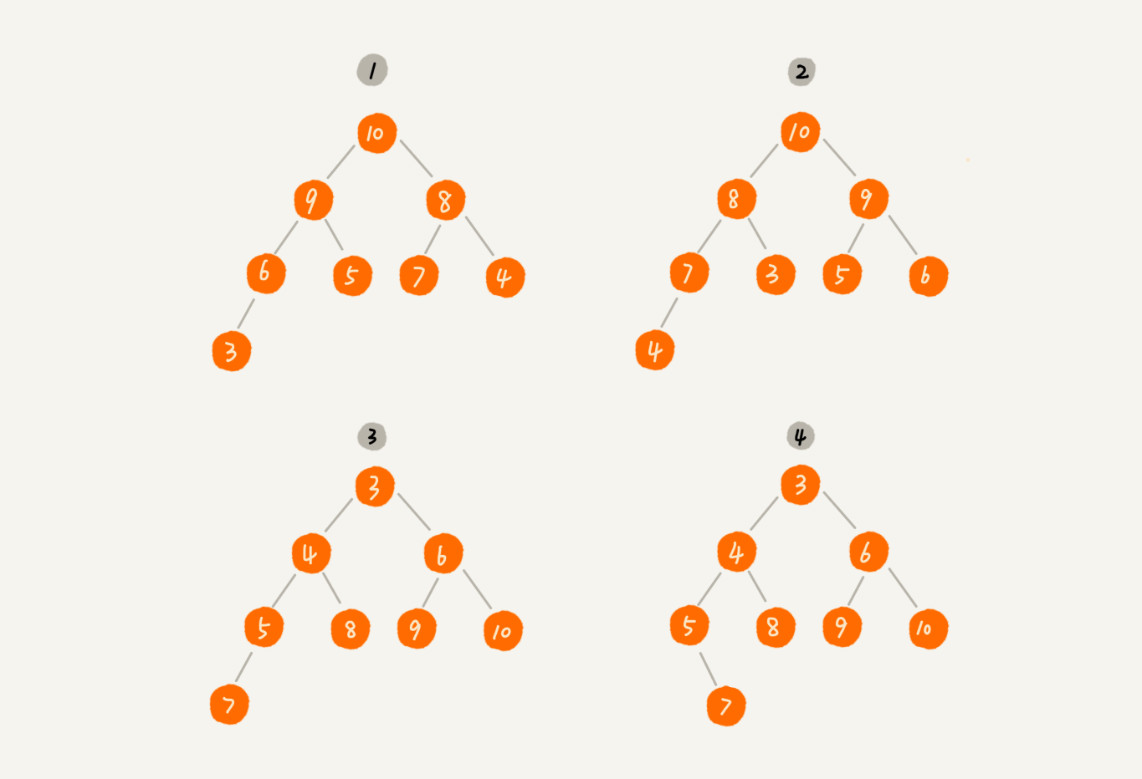
如下图所示，1、2 是大顶堆，3 是小顶堆，4 不是堆。同时，我们可以看出，对于同一组数据，可以构建出不同形态的堆。

3. 堆的存储

满足堆的一个要求是”堆是一个完全二叉树“，而完全二叉树比较适合用数组存储，一是节省空间，二是通过数组的下标就可以找到父节点、左右子节点（数组下标最好从 1 开始）。本篇讲的例子，及其代码的实现都将从数组下标为 1 的地方开始。

下面是一个用数组存储堆的例子，假如从下标 1 开始存储堆的数据，那么下标为 i 的节点的左子节点在数组中的下标为 2*i，右子节点在数组中的下标为 2*i+1，父节点在数组中的下标为 i/2。假设从下标 0 开始存储的话，下标为 i 的节点的左子节点的下标为 2*i+1，右子节点的下标为 2*i+2，父节点的下标为 (i-1)/2。

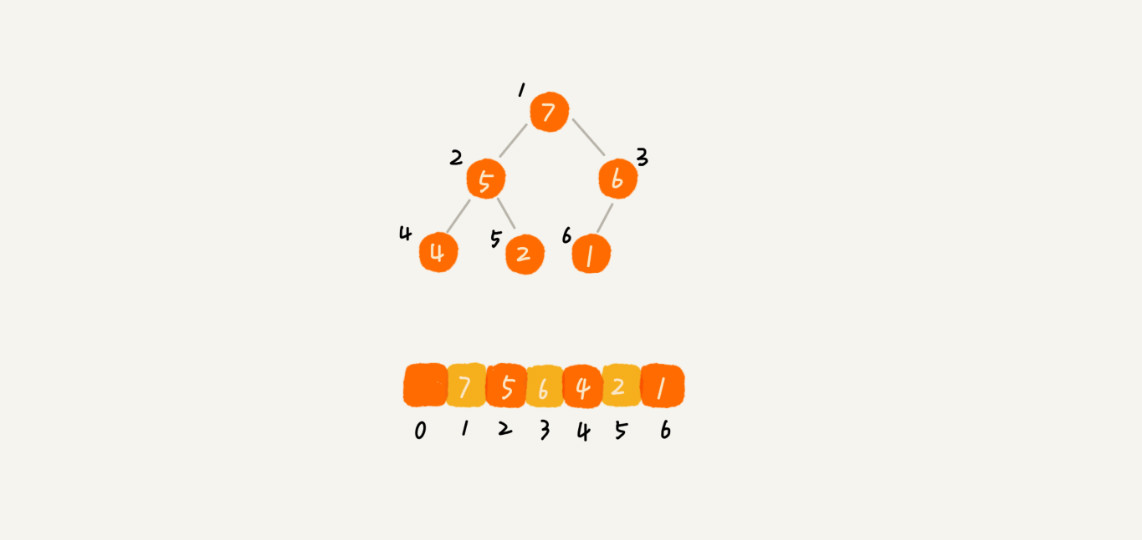
4. 堆的操作

堆最核心的操作是分别往堆中插入一个元素以及删除堆顶元素。为什么这边只提到删除堆顶元素？因为删除堆的其他元素是毫无意义，堆顶元素一般是最大或者最小值，所以删除堆顶元素才有意思。

另外，在往堆中插入一个元素或者删除堆顶元素之后，需要确保满足堆的两个特性。而将不符合两个特性的“堆”调整成符合两个特性堆的过程被称为堆化（heapify）。堆化有两种方式：从上往下堆化和从下往上堆化。两者的区别在于调整的顺序，从上往下堆化是指从堆顶元素开始向下调整使其最终符合两个特性，而从下往上则相反。在插入和删除的操作中会具体看到这两种方式。

下面的阐述都将以大顶堆为例，小顶堆同理。

4.1. 往堆中插入一个元素

插入元素时，将新插入的元素放到堆的最后比较方便。此时，采用从下往上的堆化方法比较合适，整个从下往上的堆化过程就是向上不断跟父节点对比，然后交换。如图所示，我们往一棵现成的堆中插入了一个元素 22。那么此时的“堆”不符合堆的两个特性了。那么新插入的节点先与父节点进行比较，不满足父子节点的应有的大小（大顶堆中，父节点的值应该大于子节点）则互换两个节点。互换之后的父节点和它的父节点不满足大小关系的话就继续交换。重复这个过程，直至调整过程中的父子节点都满足大小关系为止。

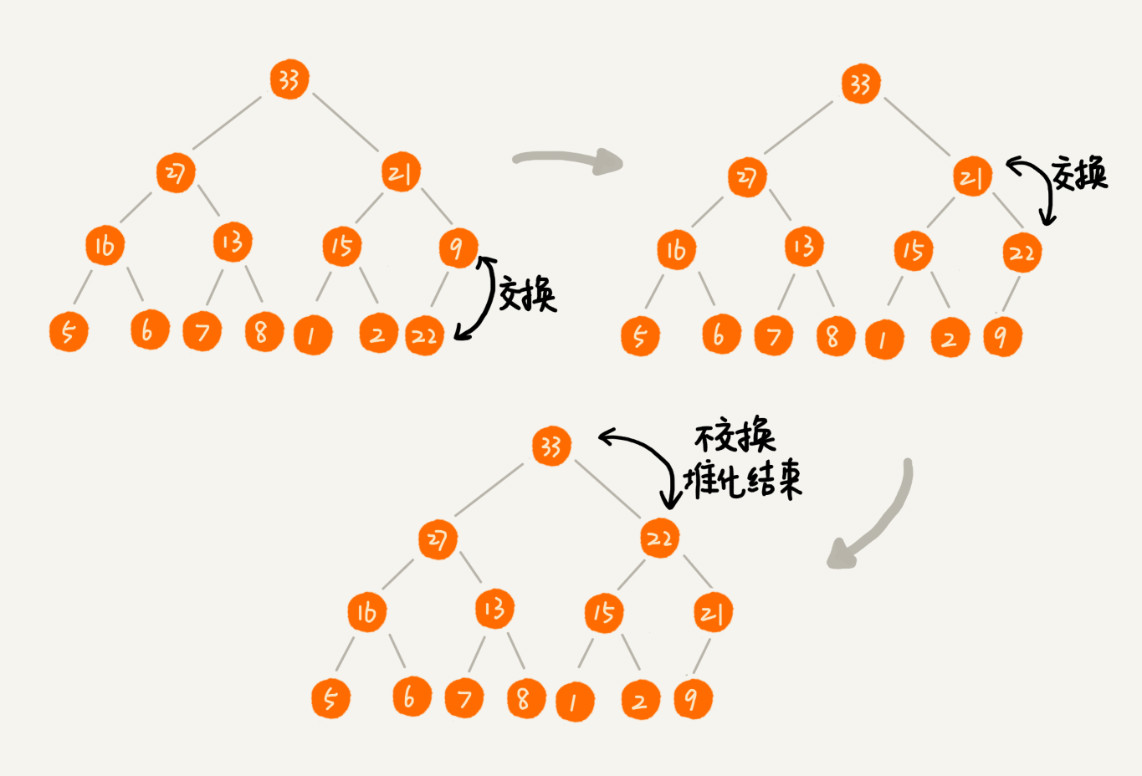
我们将这个从下到上的堆化过程，实现为如下代码段所示

public void insert(int data) {
    if (this.count >= this.capacity) {
        return;
    }
    ++this.count;
    this.heap[this.count] = data;
    heapifyFromBottom();
}

public void heapifyFromBottom() {
    int i = this.count;
    while (i/2 > 0 && this.heap[i] > this.heap[i/2]) {
        swap(i, i/2);
        i = i/2;
    }
}

4.2. 删除堆顶元素

从堆的第二点特性“堆中的每个节点的值都必须大于等于（或小于等于）其子节点的值”可以推出堆中最大（或最小）的值存储在堆顶元素中（大顶堆堆顶则是最大值）。因此删除堆顶元素是有意义的，而删除堆中的其他元素是没有意义的。

那么删除堆顶元素之后，整个堆就不符合堆的两个条件了。此时，正确的方式是把最后一个节点放到堆顶处，然后从上而下依次比较父子节点的大小，如果不满足大小关系则进行交换，直至父子节点之间满足大小关系为止。这种方法就是从上往下的堆化方法。

如图所示，假如将堆顶的元素 33 删除之后，那么将最后一个节点的元素 12 放到堆顶处。然后 12 与 27 进行比较，因为不满足大顶堆的要求，12 与 27 进行交换。以此类推，最终调整后的堆满足了所要求的两个特性。

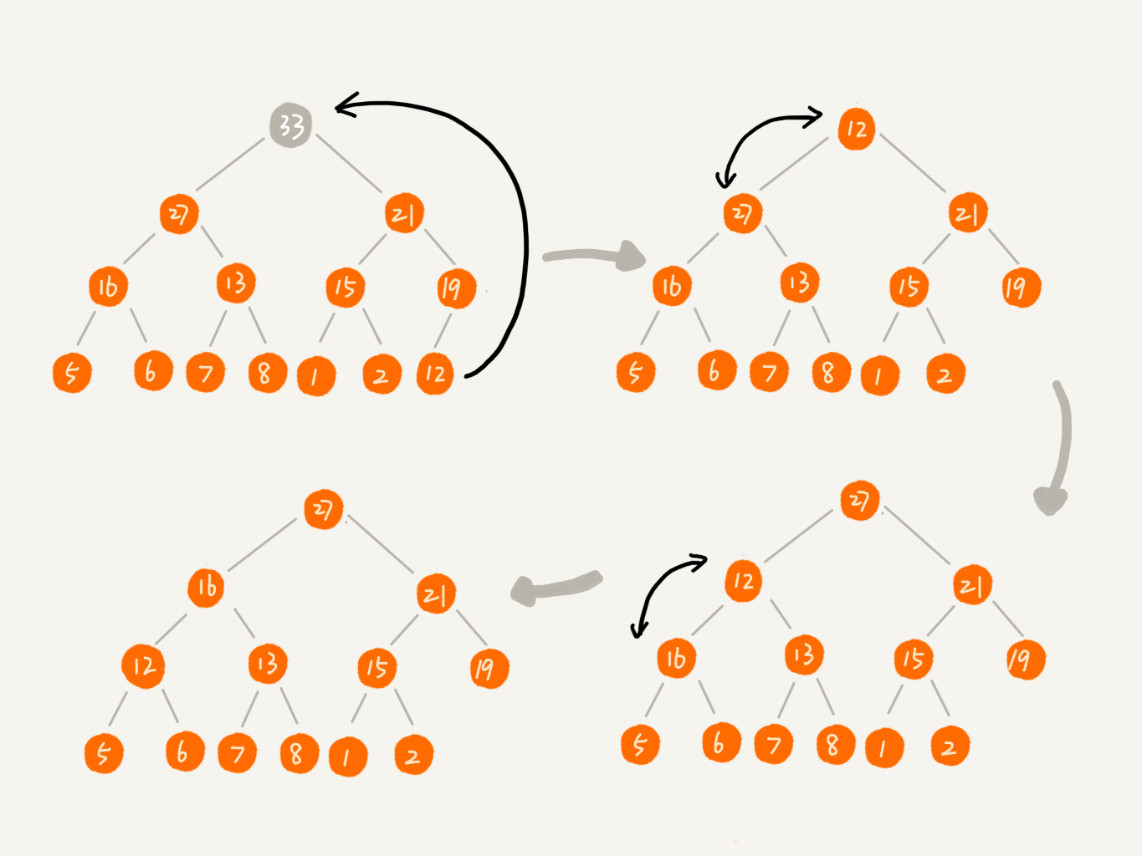
我们将上述从上而下的堆化过程实现为如下图所示

public void delete () {
    if (this.count <= 0) {
        return;
    }

    this.heap[1] = this.heap[this.count--];

    heapifyFromTop(1);
}

public void heapifyFromTop(int begin) {
    while (true) {
        int i = begin;   // i 是节点及其左右子节点中较大值的那个节点的下标

        /* 就是在节点及其左右子节点中选择一个最大的值，与节点所处的位置进行；
           但是，需要注意的是假如这个值正好是节点本身，那么直接退出循环；
           否则需要进行交换，然后从交换之后的节点开始继续堆化 */
        if (begin * 2 <= this.count && this.heap[begin] < this.heap[2 * begin]) {
            i = 2 * begin;
        }

        if ((2 * begin + 1) <= this.count && this.heap[i] < this.heap[2 * begin + 1]) {
            i = 2 * begin + 1;
        }

        if (i == begin) {
            break;
        }

        swap(begin, i);

        begin = i;
    }
}

4.3. 时间复杂度

堆化的过程是顺着节点的路径进行比较交换的，那么比较交换这一组操作的次数是跟树的层次有关的。对于一棵含 n 个节点的完全二叉树来说，树的层次不会超过 $log_2^n+1$。因此，整个堆化过程的时间复杂度是 O(logn)。那么，插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)。

5. 堆排序

借助堆这种数据结构实现的排序被称为堆排序。堆排序是一种原地的、时间复杂度为 O(nlogn) 且不稳定的排序算法。整个堆排序分为建堆和排序两个步骤。

5.1. 堆排序过程

5.1.1. 建堆

首先是将待排序数组建立成一个堆，秉着能不借助额外数组则不借助的原则，我们可以直接在原数组上直接操作。这样，建堆有两个方法：

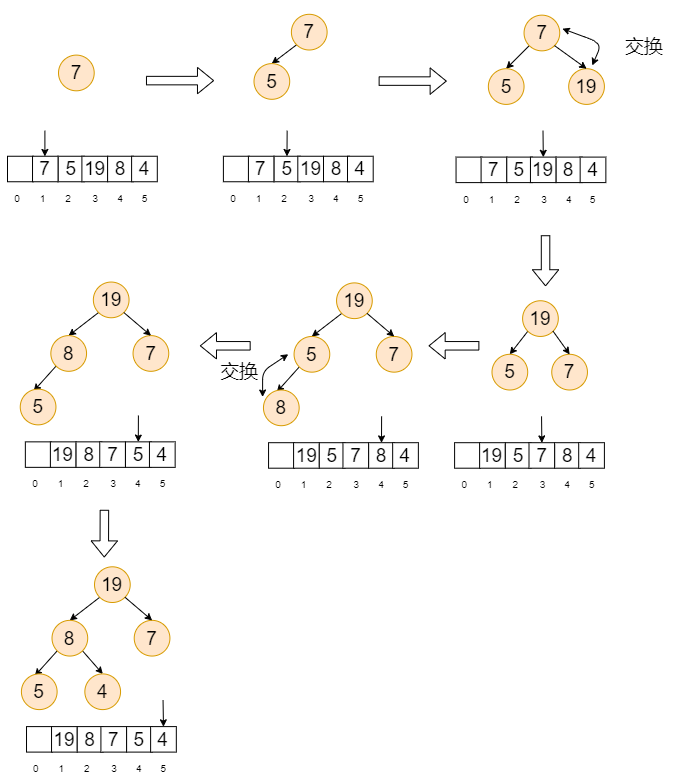
第一种方法类似于上述堆的操作中“往堆中插入一个元素”的思想。刚开始的时候假设堆中只有一个元素，也就是下标为 1 的元素。然后，将下标为 2 的元素插入堆中，并对堆进行调整。以此类推，将下标从 2 到 n 的元素依次插入到堆中。这种建堆方式相当于将待排序数组分成“堆区”和“待插入堆区”。

如图所示，我们将对待排序数据 7、5、19、8、4 进行建堆（大顶堆）。可以看到初始化堆就一个元素 7。之后将指针移到下标为 2 的位置，将 5 这个元素添加到堆中并从下往上进行堆化。之后，再将指针移到下标为 3 的位置，将 19 这个元素添加到堆中并从下往上进行堆化。依次类推。
第二种方法是将整个待排序数组都当成一个“堆”，但是这个“堆”不一定满足堆的两个条件，因此我们需要对其进行整体调整。那么，调整的时候是从数组的最后开始，依次往前调整。调整的时候，只需要调整该节点及其子树满足堆的要求，并且是从上往下的方式进行调整。由于，叶子节点没有子树，所以叶子节点没必要调整，我们只需要从第一个非叶子节点开始调整（这边的第一是从后往前数的第一个）。那么第一个非叶子节点的下标为 n/2，因此我们只需要对 n/2 到 1 的数组元素进行从上往下堆化即可（下标从 n/2 到 1 的数组元素所在节点都是非叶子节点，下标从 n/2+1 到 n 的数组元素所在节点都是叶子节点）。

如图所示，我们将对待排序数据 7、5、19、8、4、1、20、13、16 进行建堆（大顶堆）。可以看到整个过程是从 8 这个元素开始进行堆化。在对 8 进行堆化的时候，仅对 8 及其子树进行堆化。在对 5 进行堆化的时候，仅对 5 及其子树进行堆化。

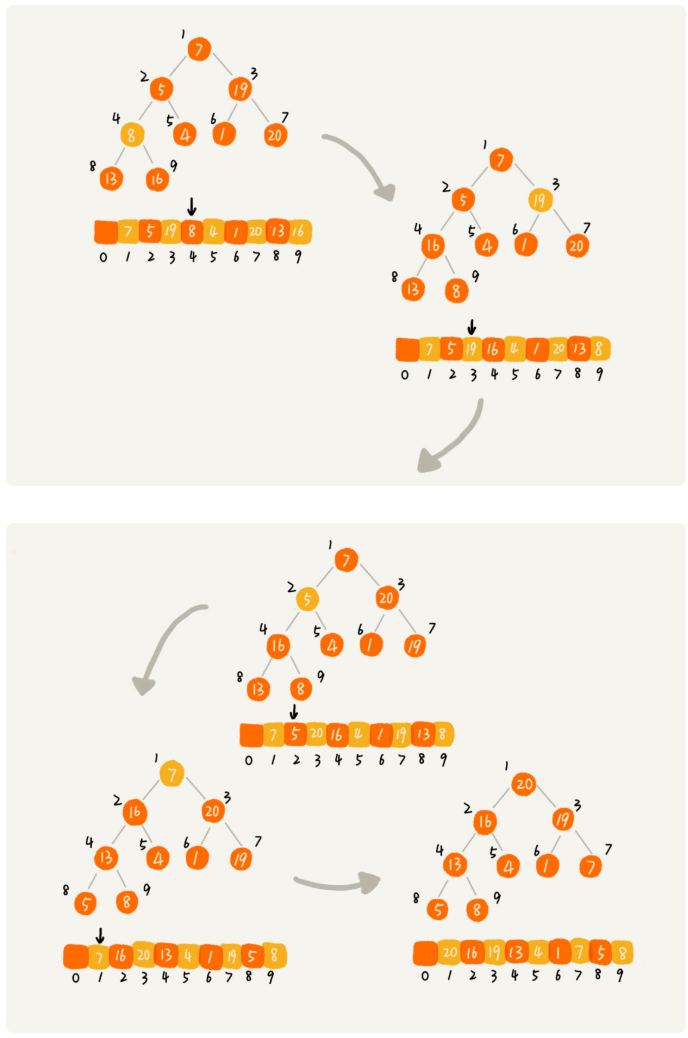
我们将第二种思路实现成如下代码段所示：

public void buildHeap(int[] datas, int len) {
    this.heap = datas;
    this.capacity = len - 1;
    this.count = len - 1;
    for (int i = this.count/2; i >=1; i--) {
        heapifyFromTop(i);
    }
}

public void heapifyFromTop(int begin) {
    while (true) {
        int i = begin;   // i 是节点及其左右子节点中较大值的那个节点的下标

        /* 就是在节点及其左右子节点中选择一个最大的值，与节点所处的位置进行；
           但是，需要注意的是假如这个值正好是节点本身，那么直接退出循环；
           否则需要进行交换，然后从交换之后的节点开始继续堆化 */
        if (begin * 2 <= this.count && this.heap[begin] < this.heap[2 * begin]) {
            i = 2 * begin;
        }

        if ((2 * begin + 1) <= this.count && this.heap[i] < this.heap[2 * begin + 1]) {
            i = 2 * begin + 1;
        }

        if (i == begin) {
            break;
        }

        swap(begin, i);

        begin = i;
    }
}

为什么下标从 n/2 到 1 的数组元素所在节点都是非叶子节点，下标从 n/2+1 到 n 的数组元素所在节点都是叶子节点？这个算是完全二叉树的一个特性。严格的证明暂时没有，不严谨的证明还是有的。这里采用反证法，假如 n/2 + 1 不是叶子节点，那么它的左子节点下标应该为 n+2，但是整个完全二叉树最大的节点的下标为 n。所以 n/2 + 1 不是叶子节点不成立，即 n/2 + 1 是叶子节点。那么同理可证 n/2 + 1 到 n 也是如此。而对于下标为 n/2 的节点来说，它的左子节点有的话下标应该为 n，n 在数组中有元素，因此 n/2 有左子节点，即 n/2 不是叶子节点。同理可证 1 到 n/2 都不是叶子节点。

5.1.2. 排序

建完堆（大顶堆）之后，接下去的步骤是排序。那么具体该怎么实现排序呢？

此时，我们可以发现，堆顶的元素是最大的，即数组中的第一个元素是最大的。实现排序的过程大致如下：我们把它跟最后一个元素交换，那最大元素就放到了下标为 n 的位置。此时堆顶元素不是最大，因此需要进行堆化。采用从上而下的堆化方法（参考删除堆顶元素的堆化方法），将剩下的 n-1 个数据构建成堆。最后一个数据因为已知是最大了，所以不用参与堆化了。n-1 个数据构建成堆之后，再将堆顶的元素（下标为 1 的元素）和下标为 n-1 的元素进行交换。一直重复这个过程，直至堆中只剩一个元素，此时排序工作完成。如图所示，这是整个过程的示意图。

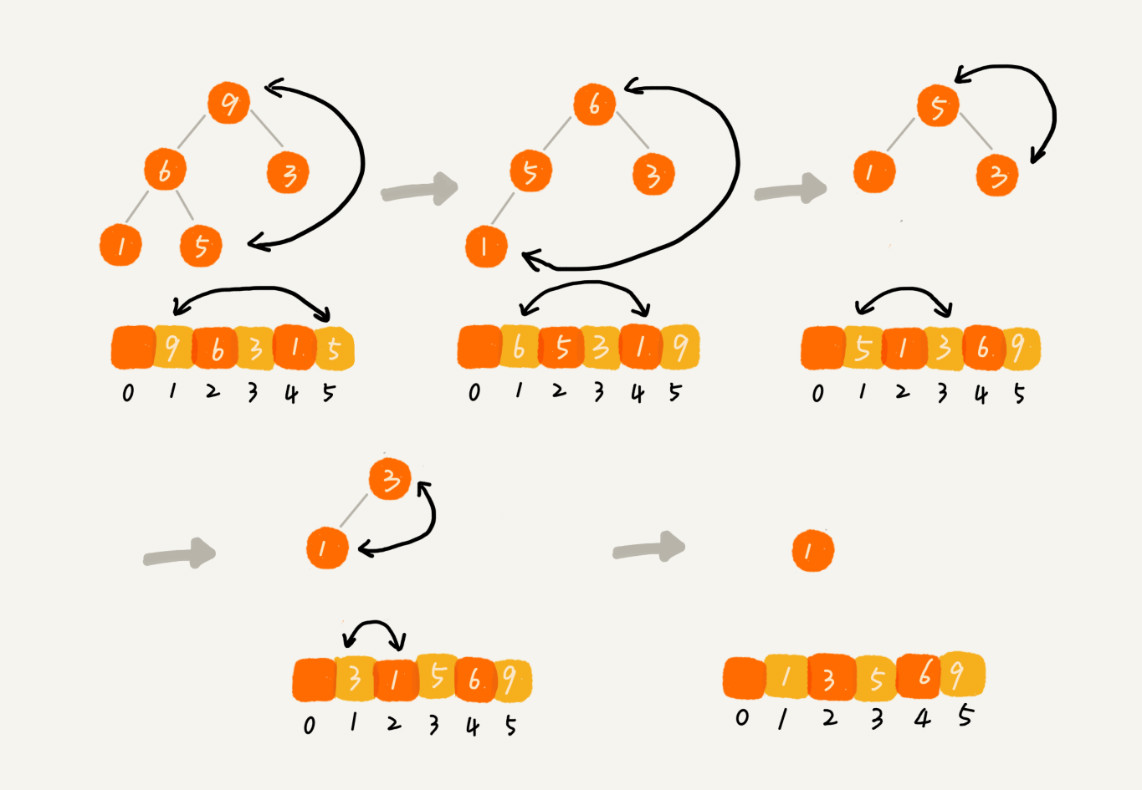
下面将这个过程使用 Java 实现，如下图所示

public void heapSort() {
    while (this.count > 1) {
        swap(this.count, 1);
        this.count--;
        heapifyFromTop(1);
    }
}

5.2. 算法分析

5.2.1. 时间复杂度

堆排序的时间复杂度是由建堆和排序两个步骤的时间复杂度叠加而成。

建堆的时间复杂度

在采用第二方式建堆时，从粗略的角度来看，每个节点进行堆化的时间复杂度是 O(logn)，那么 n/2 个节点堆化的总时间复杂度为 O(nlogn)。但是这此时粗略的计算，更加精确的计算结果不是 O(nlogn)，而是 O(n)。

因为叶子节点不需要进行堆化，所以需要堆化的节点从倒数第二层开始。每个节点需要堆化的过程中，需要比较和交换的次数，跟这个节点的高度 k 成正比。那么所有节点的高度之和，就是所有节点堆化的时间复杂度。假设堆顶节点对应的高度为 h ，那么整个节点对应的高度如图所示（以满二叉树为例，最后一层叶子节点不考虑）。

那么将每个非叶子节点的高度求和为
$$
S_1 = 1h + 2^1(h-1) + ...+ 2^{k(h-k) +...+2}1
$$
求解这个公式可将两边同时乘以 2 得到 S2，
$$
S_2 = 2^1h + 2^{2(h-1) + ... + 2}(h-k+1) + ... + 2^{*(2) + 2}h*1
$$
然后再减去 S1，从而就得到 S1
$$
s_1 = -h +2^{1 + 2}2 +...+2⁺²h=2^{{h+1}-h-2

$$

由于

$$

h=log_2}n
$$
所以最终时间复杂度为 O(2n-logn)，也就是 O(n)。

排序的时间复杂度

排序过程中，我们需要进行 (n-1) 次堆化，每次堆化的时间复杂度是 O(logn)，那么排序阶段的时间复杂度为 O(nlogn)。

总的时间复杂度

那么，整个总的时间复杂度为 O(nlogn)。

不对建堆过程的时间复杂度进行精确计算，也就是建堆以 O(nlogn) 的时间复杂度算的话，那么总的时间复杂度还是 O(nlogn)。

5.2.2. 稳定与否

堆排序不是稳定的排序算法。因为在排序阶段，存在将堆的最后一个节点跟堆顶点进行互换的操作，所以有可能会改变相同数据的原始相对顺序。比如下面这样一组待排序 20、16、13、13 ，在排序时，第二个 13 会跟 20 交换，从而更换了两个 13 的相对顺序。

5.2.3. 是否原地

堆排序是原地排序算法，因为堆排序的过程中的两个步骤中都只需要极个别临时存储空间。

5.3. 堆排序总结

在实际开发中，为什么快速排序要比堆排序性能要好？

对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序

对于基于比较的排序算法来说，整个排序过程就是由比较和交换这两个操作组成。快速排序中，交换的次数不会比逆序度多。但是堆排序的过程，第一步是建堆，这个过程存在大量的比较交换操作，并且很有可能会打乱数据原有的相对先后顺序，导致原数据的有序度降低。比如，在对一组已经按从小到大的顺序排列的数据进行堆排序时，那么建堆过程会将这组数据构建成大顶堆，而这一操作将会让数据变得更加无序。而采用快速排序的方法时，只需要比较而不需要交换。

最直接的方式就是做个试验看一下，对交换次数进行统计。
堆排序的访问方式没有快速排序友好

快速排序来说，数据是顺序访问的。而堆排序，数据是跳着访问的。访问的数据量如何很大的话，那么堆排序可能对 CPU 缓存不太友好。

6. 堆的其他应用

上面介绍了堆的理论和堆排序，但是堆这种数据结构除了用在堆排序之外，还有其他几个非常重要的应用：优先级队列、求 Top K 问题以及求中位数问题。

6.1. 优先级队列

优先级队列跟普通队列所有不同。普通队列最大的特性是先进先出，而优先级队列则按照优先级来，优先级高的先出队。我们可以发现，优先级队列和堆有共通之处。堆顶元素都是最大或者最小的，那么取堆顶元素就类似于优先级队列的出队操作。因此，优先级队列最直接、最高效的实现方式是采用堆来实现。

很多语言也都有提供优先级队列的实现，比如 Java 的 PriorityQueue，C++ 的 priority_queue 等。当然，优先级队列也有很多应用场景，这边举两个简单的例子来看一下优先级队列是怎么用的。

6.1.1. 合并有序小文件

假设我们需要将 100 个存储着有序的单词的文件合并成一个有序的大文件。按照之前讲过的方法，我们可以使用数组的方式，也就是从这个 100 个文件中，各取第一个单词。之后，根据字典序进行比较，将字典序最小的那个单词放入合并后的大文件，并从数组中删除。然后，从删去单词的那个小文件中再取一个单词，将其放入数组。之后重复上述操作，直至 100 个文件的单词都被合并到最终的有序的大文件中。使用数组这种方式，每次取字典序最小的那个单词时都需要遍历整个数组。显然，数组的方式很不高效。

那么我们可以使用优先级队列，因为我们每次需要的都是当前字典序最小的那个单词，这跟优先级队列的特性很相似。因此，我们可以维护一个容量为 100 的小顶堆，每次取小顶堆的堆顶单词，然后将其放入合入的大文件中，之后再从小文件中取新的单词放入堆中，并进行堆化。重复这个过程，最终将 100 个文件的单词数据全都合并到大文件中。那么采用堆的方式之后，每次取字典序最小单词的时间主要就是堆化的时间，而堆化的时间复杂度是 O(logn)，这边 n 是 100。显然这个时间比使用数组的方式高效多了。

6.1.2. 高性能定时器

假设有一个定时器，定时器维护了很多任务。每个任务都设定了一个要触发执行的时间点。普通的方法可能就是采用轮询的方式。每隔一段时间轮询一次（比如 1 秒），查看是否有任务到达设定的执行时间。如果到达了，就拿出来执行。然而，这种做法比较低效。一是可能有些任务执行还要很久的时间，那么前面很多次的扫描将是徒劳的；二是当任务列表很大的时候，每次这么扫描是很费时的。

那么我们照样可以使用优先级队列。我们按照任务设定的执行时间构建小顶堆，堆顶元素是任务设定的执行时间距离现在最近的任务，也就是应该最先被执行的任务。当我们拿到堆顶任务的执行时间点之后，与现在的时间进行相减，从而得到一个时间间隔 T1 。接下去，我们就可以不用每隔 1 秒进行扫描，而是在 T1 秒之后，直接取堆顶的任务来执行。并且，对剩下的任务进行堆化，再计算新的堆顶任务距离现在的时间间隔 T2，将其作为执行下一个任务需要等待的时间，以此类推。采用这种方式后，性能相比每隔 1 秒的轮询方式提高了许多。

6.2. 求 Top K

求 Top K 的问题可以分为两类，一类是针对静态数据集合，也就相当于这个数据集合事先确定了，不会再变了。另一类是针对动态数据集合，也就是说数据事先并不完全确定，会有数据不断的加入到集合中。下面针对这两类分别进行阐述，求 Top K 大的问题为例。

针对静态数据，使用堆来求 Top K 的方法如下。

我们需要维护一个大小为 K 的小顶堆。一开始的时候，我们可以拿数组前 K 个元素先将这个堆填满，也就相当于用前 K 个元素先构建一个小顶堆。之后，顺序遍历数组剩下的元素。如果，遍历到的元素大于堆顶元素，则将原堆顶元素替换为遍历到的元素，然后丛上而下的方式进行堆化。如果比堆顶元素小，则不做处理，继续遍历。当遍历完成之后，堆中的元素则是前 Top K 大的数据了。

对前 k 个数据构建堆时，时间复杂度为 O(k)，那么假设剩下的 n-k 个数据在遍历之后都需要加入堆并进行堆化，那么这个的时间复杂度为 O((n-k)logk)。总的时间复杂度应该为 O((n-k)logk + k)。简单粗暴点来说，假如在对前 k 个数据构建堆时，是按照“往堆中插入一个元素”的方式的话，那么时间复杂度也可以算作 O(nlogk)。
针对动态数据，使用堆来求 Top K 的方法如下。

同样，我们需要维护一个大小为 K 的小顶堆。一开始的时候，当堆中数据不满 K 个的时候，每当插入一个数据之后，就将其放入堆中。当堆中数据满 K 个之后，如果有新的数据被添加到集合中时，那么先与堆顶元素进行比较。如果大于堆顶元素，则将堆顶元素替换为新数据，然后进行堆化。如果小于堆顶元素，则不做处理。这样，无论什么时候查询时堆中的元素始终是 Top K 大的。

当然还有另一种方法是，在每次查询的时候再针对新的数据集合求 Top K 问题，采用针对静态数据的方式。

个人觉得这种方式和另一种方式，要具体问题具体分析。比如查询时间比较短，前面第一种的实时方式比较合适。查询时间比较长，并且新数据增加特别快，那么第二种方式比较合适。

快速排序也能求 Top K 的问题，但是快速排序更加适合于静态数据，如果数据集合一直在变动，那堆的方式会更适合一点。

另外在 Top K 的问题上，快排和堆这两种方式，堆会更胜一筹。

6.3. 求中位数及各种百分位的数据

中位数是按顺序排列的一组数据中居于中间位置的数。如果数据的个数是奇数，那么中位数的位置为 n/2+1（数据是从 1 开始编号，n 是最后一个数据的编号）。如果数据的个数是偶数，那么中位数的位置为 n/2 或者 n/2 +1（同上），一般情况下是取这两个数的平均值作为中位数，当然也可以取 n/2 位置的数据作为中位数。下面我们选择这两个数的平均值作为中位数为例。

针对一组静态数据，求中位树的最好方式就是先排序，然后再取中位数。假如有查询中位数的操作时，可以将第一次求得中位数的值缓存下来或者中位数的位置缓存下来。
针对动态数据集合时，集合不断地变动，中位数也不断的变动。那么，再用先排序再求中位数的方式，效率就不高了。为此，我们可以使用堆这种数据结构，并且维护两个堆，一个大顶堆，一个小顶堆。大顶堆存储前一半的数据，小顶堆存储后一半的数据。大顶堆中的数据都比小顶堆中的数据小，也就是大顶堆的堆顶数据小于等于小顶堆的堆顶数据（有点类似沙漏）。

如图所示，假如 n 是奇数，那么 n/2+1 个数据全都存储在大顶堆中，剩下的 n/2个数据存储在小顶堆中。这样，大顶堆的顶堆数据就是中位数（当然 n/2 个数据全都存储在大顶堆，剩下的 n/2 + 1 个数据存储在小顶堆中也行，那么小顶堆的顶堆数据就是中位数）。假如 n 是偶数，那么前 n/2 个数据全都存储在大顶堆中，剩下的 n/2 个数据存储在小顶堆中。那么大顶堆的堆顶数据和小顶堆的堆顶数据求平均就是中位数了。

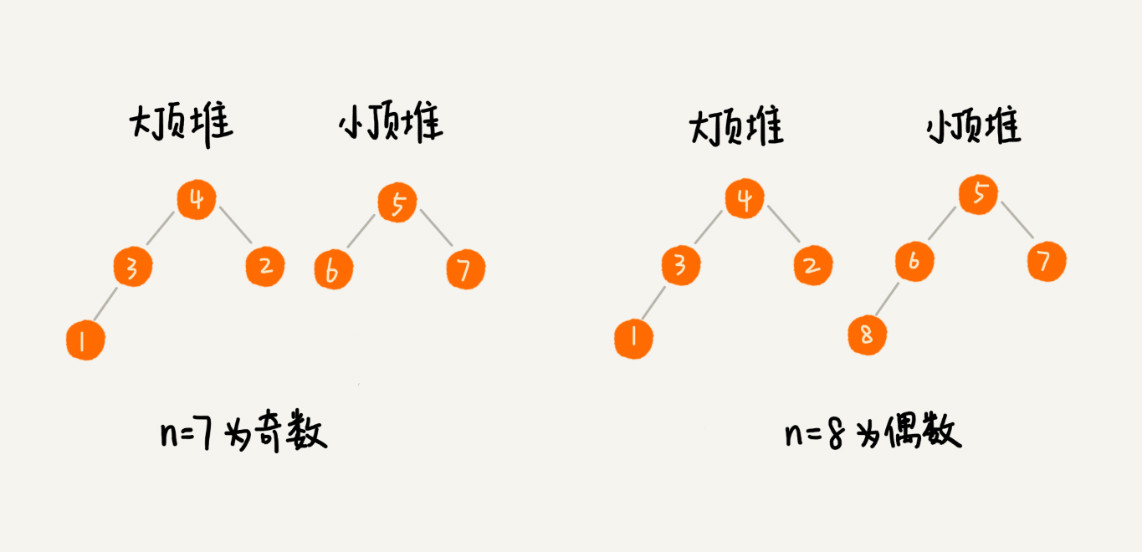
那么当插入新的数据时，如果这个数据比大顶堆的数据小，那么则将其插入大顶堆。反之，则将其插入小顶堆。同时，插入新的数据之后需要确保两个堆的数据数量比例按照约定来，即插入之后如果数据数量为偶数，那么两个堆的数量需要相等；如果数据数量为奇数，那么大顶堆要比小顶堆多一个数据。假如插入数据之后，两个堆的数据数量不符合约定了，那么则需要移动数据使其满足约定，移动的数据一般都是堆顶元素。

使用这种方法，插入数据的时候会涉及到堆化，时间复杂度为 O(logn)，但是在求中位数的时候，只需要 O(1)。因此，个人觉得跟上述求 Top K 的类似。如果查询中位数很频繁，那么动态方式的方式很 nice 了；假如查询中位数不频繁，那么静态的方式可能会更好。

另外，动态数据集合使用两个堆来求中位数的方法也可以很好地用于求其他百分位的数据。求中位数其实就相当于求 50% 处的数据。比如，当求 90% 处的数据时。我们可以 90% 的数据保存在大顶堆中，10 % 的数据保存在小顶堆中。同样的，插入数据之后也要维护两个堆的比例，并且插入的时间复杂度为 O(logn)，而查询的时间复杂度为 O(1)。

这边一定需要两个堆吗？我觉得是需要的，比如在查找 90% 的数据时，虽然我们都只需要取大顶堆的堆顶元素。但是，假如我们只维护一个大顶堆。某次插入数据时，这个数据没被插入到大顶堆中，结果导致大顶堆和剩下的元素不符合比例了（比如大顶堆比应有的少了一个数据，而小顶堆比应有的多了一个数据）。那么我们需要从剩下的数据中找出在剩下的数据中最小的那个数据插入大顶堆。此时，假如剩下的数据直接使用小顶堆的方式来表示，那么只需要取堆顶元素即可，很方便。这个使用堆的方式和数组的方式，在合并有序小文件的时候已经做过比较了。所以需要两个堆！

7. 总结

堆是一种很重要的数据结构。堆满足两个特性，一是完全二叉树，二是任意节点都比其子节点大（或者小）。任意节点都比其子节点大的叫做大顶堆，否则叫做小顶堆。由于堆是一个完全二叉树，所以堆使用数组的方式存储会更加合适。因此，我们对堆的操作一般都是在基于数组完成的。
堆常见的操作是插入元素和删除堆顶元素（注意：删除堆中的其他元素是没有意义的）。另外，插入和删除元素之后大部分情况下都是需要进行堆化的，堆化的时间复杂度是 O(logn)，因此这两个操作的时间复杂度都是 O(logn)。
堆最常见的应用是堆排序。使用堆排序对一组数据集合进行排序时，分为两步骤：①先是建堆。建堆就是将这组数据结合建立成一个堆，这里可以不用开辟新的内存空间而基于原数据集合直接建立堆。基于原数据集合直接建立堆可以采用两种方式，一种是从头往后开始遍历数组，这种方式类似于往堆中插入数据；另一种则是从后往前，从最后一个非叶子节点开始对该非叶子及其子树进行从上往下的堆化。②再是排序。由于堆顶的元素是最值，因此先将堆顶元素和最后一个元素交换，然后将堆中的数量减一（相当于把位于最后位置的堆顶元素给删除了）。之后再对剩下的数据进行堆化。堆化完成之后，再取堆顶元素，再交换，以此类推。最终实现排序。

堆还有其他几种常见的应用。①优先级队列。优先级队列中，优先级最高的会先出队，这跟堆的本质是一样的。那么优先级队列可用于多个有序小文件的合并，同理也适合于多个有序数组的合并。②求 Tok K 问题。Top K 问题也可以使用快速排序的方式实现求解。但是，总体来看堆更适合用于求 Top K 问题，尤其针对动态数据集合。堆求 Top K 主要是维护一个容量为 K 的小顶堆，当遍历到的数据比堆顶元素大则加入堆，反之什么也不做。③求中位数或者各种百分位的数据。此时，我们应该维护两个堆，一个大顶堆，一个小顶堆。大顶堆中的元素都比小顶堆中的元素小。两个堆中的数据比例要符合所求的百分位情况。比如中位数，就两个堆中的数据比例要占 50%。比如 90% 位的数据，那么小顶堆中的数据占 90%，大顶堆中的数据占 10%。那么，小顶堆的堆顶元素就是 90% 位的数据。另外，当两个堆的数据占比不符合约定时，需要进行数据的移动。

对应用在求 Top K 和中位数时，发现针对动态数据集合效果会更显著。由此，我们可以想到，堆这种数据结构可能更适合一些动态数据集合的场景。

巨人的肩膀

极客时间专栏，王争老师的《数据结构与算法之美》

附 Github

整个系列的代码可查看 github 仓库 https://github.com/DawnGuoDev/algos ，这个仓库将主要包含常用数据结构及其基本操作的手写实现（Java），也会包含常用算法思想经典例题的实现（Java）。在接下来一年内，这个仓库将会保持更新状态，在此之间学到的关于数据结构和算法的知识或者实现也都会往里面 commit，所以赶紧来 star 哦。