机器学习局 | 朴素贝叶斯-文本界的扛把子

1.知识铺垫

在真正的讲解朴素贝叶斯模型之前，想先讲一些在该模型中会涉及到的一些概率论知识。

1.1 等可能概型

等可能概型是指试验中的样本空间只包含有限个元素并且试验中每个基本事件发生的可能性相同，公式如下

$$P(A)=\frac{事件A中包含的基本事件数}{S中包含的基本事件数}$$

其中S是指随机试验E的所有可能结果组成的集合，也就是E的样本空间。

1.2 条件概率

条件概率是指在事件A已发生的条件下事件B的概率，记为$P(B|A)$，其中

$$P(B|A) = \frac{P(AB)}{P(A)}$$

怎么去理解上述这个条件概率的计算公式呢，相比等可能概型的来说，因为$P（B|A）$是指在事件A发生的情况下事件B发生的情况，所以

$$\begin{aligned} P(B|A)=&\frac{在A情况下B事件总数}{A情况下的事件总数}\\ =&\frac{\frac{在A情况下B事件总数}{S中包含的基本事件数}}{\frac{A情况下的事件总数}{S中包含的基本事件数}}\\ =&\frac{P(AB)}{P(A)} \end{aligned}$$

1.3 全概率公式

设S为试验E的样本空间，$B_1,B_2,...,B_n$为E的一组事件，若满足以下两个条件

• $B_iB_j=\phi,i\neq j;i,j=1,2,...,n$
• $B_1\bigcup B_2\bigcup ...B_n=S$

那么$B_1,B_2,...,B_n$为样本空间S的一个划分。举个例子，如下图所示：

A’,A为E的两个事件，并且满足上述条件，那么A’,A就是为样本空间S的一个划分。

插播一个不正式的理解方法：划分就可以当成分蛋糕一样，样本空间S即为整块蛋糕

在了解划分的定义之后，说一下全概率公式，假如试验E的样本空间为S，A为E的事件，$B_1,B_2,...,B_n$为S的一个划分，且$P(B_i)>0(i=1,2,...,n)$，那么全概率公式为

$$\begin{aligned} P(A) =&P(AS)\\ =&P(A(B_1\cup B_2\cup ... \cup B_n ))\\ =&P(AB_1\cup AB_2 \cup... \cup AB_n)\\ =& P(AB_1)+P(AB_2)+...+P(AB_n)\\ =&P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+...+P(A|B_n)P(B_n) \end{aligned}$$

1.4 贝叶斯公式

对于较为特殊的贝叶斯公式来说：

$$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$$

知道上述的贝叶斯公式之后，我们讨论较为一般的贝叶斯公式，设试验E的样本空间为S，A为E的事件，$B_1,B_2,...,B_n$为S的一个划分，且$P(A)>0$,$P(B_i)>0(i=1,2,...,n)$，则一般化的贝叶斯公式如下

$$\begin{aligned} P(B_i|A) =& \frac{P(A|B_i)P(B_i)}{P(A)}\\ =&\frac{P(A|B_i)P(B_i)}{\sum_{j=1}^{n}P(A|B_j)P(B_j)}，i=1,2,...,n \end{aligned}$$

然而上面的贝叶斯公式中概率都是离散的，实际上贝叶斯公式一样可以应用于连续概率的情况，假设上面的具体事件的概率不是一个确定值而是一个概率密度函数，那么连续概率的贝叶斯定理的形式为

$$f(x|y) = \frac{f(y|x)f(x)}{\int_{-\infty}^{+\infty}f(y|x)f(x)dx}$$

下面举一个关于贝叶斯应用的简单例子：

假设事件A是指客人中会喝酒的，且P(A)=0.1；假设事件B是指客人中会开车的，且P(B)=0.2；已知客人中会开车的人中有5%的会喝酒，即P(A|B)=0.05，求客人中会喝酒的人中会开车的概率是多大，即求P(B|A)

$$P(B|A) = \frac{P(A|B)P(B)}{P(A)} = 0.1$$

1.5 独立事件

设A,B为两事件，如果满足等式：

$$P(AB)=P(A)P(B)$$

则称事件A,B相互独立，简称A,B独立。

两事件相互独立的含义是其中一个事件已经发生，不影响另一个发生的概率。并且对于独立事件，我们往往是根据实际意义加以判断的。

1.6 先验概率&&后验概率

如下面公式所示：

$$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$$

• P(B)称为“先验概率”，即在A事件发生之前，我们对B事件概率的一个判断；

• P(B|A)称为“后验概率”，即在A事件发生之后，我们对B事件概率的重新估计；

一般后验概率在实际中很难直接算出来，但是先验概率就容易多了，因此一般会利用先验概率来计算后验概率。

维基百科：
在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率（Posterior probability）是在考虑和给出相关证据或数据后所得到的条件概率。

2. 朴素贝叶斯模型

2.1 贝叶斯决策论

朴素贝叶斯是贝叶斯决策论的一部分，所以在讲述朴素贝叶斯之前有必要提一下贝叶斯决策论。贝叶斯决策论是概率框架下实施决策的基本方法。对分类任务来说，在所有相关概率都已知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。那么简单来说的话就是利用贝叶斯公式，对于公式

$$P(c|\textbf{x})=\frac{P(c)P(\textbf{x}|c)}{P(\textbf{x})}\\ \textbf x=(x_1,x_2,...,x_n)$$

来说，P©是类“先验”概率，$P(\textbf{x}|c)$是样本x相对于类别标记c的类条件概率，P(x)是用于归一化的“证据因子”，然而对于给定的样本x，证据因子与类标记无关，所以基于训练数据D来估计先验概率P©和条件概率$P(\textbf{x}|c)$就可以估计出$P(c|\textbf{x})$的大小，之后比较$P(c|\textbf{x})$的大小，概率较大的那个类别即为判断的类别。如$P(c_1|\textbf{x})>P(c_2|\textbf{x})$，那么类别为c_1。

2.2 朴素贝叶斯模型

上面讲解了贝叶斯决策论，那么对于贝叶斯和朴素贝叶斯不同的之处在于“朴素”二字。因为对于[2.1 贝叶斯决策论](#2.1 贝叶斯决策论)中提到的公式来说，后验概率$P(c|\textbf{x})$的主要困难之处在于类条件概率$P(\textbf{x}|c)$是所有属性上的联合概率，直接根据样本出现的频率来估计将会遇到严重的困难。例如，假设样本的d个属性都是二值的，则样本空间将有$2^d$种可能的取值，在现实应用中，这个值往往远大于训练样本数m，也就是说很多样本取值在训练集中根本没有出现，那么就难以从有限的训练样本直接估计而得。为了避开这个障碍，朴素贝叶斯采用了下面两个假设：

• 属性条件独立性假设，即对已知类别，假设所有属性相互独立。
• 每个属性同等重要

所以对于类条件概率$P(\textbf{x}|c)$而言，在每个属性都是相互独立的条件下有

$$\begin{aligned} P(\textbf{x}|c) =& P(x_1,x_2,...,x_n|c)\\ =&P(x_1|c)P(x_2|c)...P(x_n|c)\\ \end{aligned}$$

从而推得

$$P(c|\textbf{x})=\frac{P(c)\prod_{i=1}^{n}P(x_i|c)}{P(\textbf{x})}$$

其中n为属性数目，$x_i为\textbf{x}$在第i个属性上的取值，c为最终的类别。那么上述这个式子就是朴素贝叶斯的模型函数。显然，朴素贝叶斯分类器的训练过程就是基于训练集D来估计先验概率$P(c)$和每个属性的条件概率$P(x_i|c)$，得到这些值之后，那么就可以进行预测了。同理，如果在取得这些值之后如果得到$P(c_1|\textbf{x})>P(c_2|\textbf{x})$，那么类别为c_1。下面就来具体讲解如何获得所需要的值。

一句话概括朴素贝叶斯模型函数就是：在训练样本的基础上做一系列概率运算，然后用这些算出来的概率按朴素贝叶斯公式“拼装”成分类模型——这就成了朴素贝叶斯分类器。

3. 朴素贝叶斯的求解

3.1 先验概率和属性的条件概率计算

对先验概率$P(c)$而言，令$D_c$表示训练集D中第c类样本组成的集合，若有充足的独立同分布样本，则可容易地估计该概率。

$$P(c) = \frac{|D_c|}{|D|}$$

若是离散属性，令$D_{c,x_i}表示D_c中在$第i个属性上取值为$x_i$的样本组成的集合，则条件概率

$$P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}$$

但是为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”，如$P(x_2|c) = 0 $时，连乘之后那么整个计算出来的概率值为零。所以在估计概率值时通常要进行“平滑”处理，常用“拉普拉斯修正”，具体来说，令N表示训练集D中可能的类别数，$N_i$表示第i个属性可能的取值数，则上述式子修正为：

$$P(c) = \frac{|D_c|+1}{|D|+N}\\ P(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}$$

通过拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题。并且在训练集变大时，修正过程所引入的先验的影响也会逐渐变得可忽略，使得估值逐渐趋向于实际概率值。

其他属性携带的信息被训练集中未出现的属性值“抹去”，对于这个现象，可以看下文[3.2 举例](#3.2 举例)中的讲解。

对于连续属性可考虑概率密度函数，假设$p(x_i|c)\sim \mathcal N(\mu _{c,i},\sigma^2_{c,i})$，其中$\mu _{c,i}和\sigma^2_{c,i}$分别是第c类样本在第i个属性上取值的均值和方差，则有

$$p(x_i|c) = \frac{1}{\sqrt{2\pi}\sigma_{c,i}}exp(-\frac{(x_i-\mu _{c,i})^2}{2\sigma_{c,i}^2})$$

3.2 举例

全部数据集如下图所示：

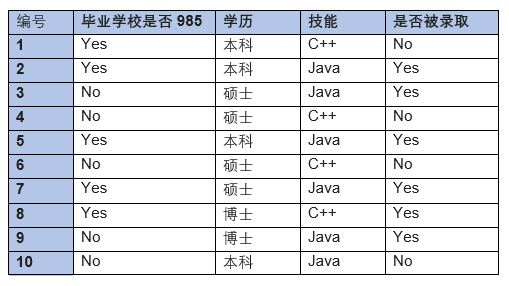
对应符号表达含义以及计算出来的相关概率如下所示，关于概率的计算我们还是采用未经过“拉普拉斯修正”的概率：

$$\begin{aligned} &c_1：被录取；c_2：不被录取；\\ &f_{11}：是985毕业；f_{12}：不是985毕业；\\ &f_{21}：本科；f_{22}：硕士；f_{23}：博士；\\ &f_{31}：技能为C++；f_{32}：技能为Java\\ &P(C=c_1)=0.6\\ &P(C=c_2)=0.4\\ &P(F_1=f_{11}|C=c_1)=0.67\\ &P(F_1=f_{12}|C=c_1)=0.33\\ &P(F_2=f_{21}|C=c_1)=0.33\\ &P(F_2=f_{22}|C=c_1)=0.33\\ &P(F_2=f_{23}|C=c_1)=0.33\\ &P(F_3=f_{31}|C=c_1)=0.17\\ &P(F_3=f_{32}|C=c_1)=0.83\\ &P(F_1=f_{11}|C=c_2)=0.25\\ &P(F_1=f_{12}|C=c_2)=0.75\\ &P(F_2=f_{21}|C=c_2)=0.5\\ &P(F_2=f_{22}|C=c_2)=0.5\\ &P(F_2=f_{23}|C=c_2)=0\\ &P(F_3=f_{31}|C=c_2)=0.75\\ &P(F_3=f_{32}|C=c_2)=0.25\\ \end{aligned}$$

假如这时候一个样本x的属性值为$f_{11},f_{22},f_{31}$(985毕业，硕士，技能C++)，那么：

$$\begin{aligned} P(C=c_1|\textbf{x})∝&P(C=c_1)P(F_1=f_{11}|C=c_1)P(F_2=f_{22}|C=c_1)P(F_3=f_{31}|C=c_1)\\ =&0.6∗0.67∗0.33∗0.17=0.022; \end{aligned}$$

$$\begin{aligned} P(C=c_2|x)∝&P(C=c_2)P(F_1=f_{11}|C=c_2)P(F_2=f_{22}|C=c_2)P(F_3=f_{31}|C=c_2)\\ =&0.4∗0.25∗0.5∗0.75=0.038 \end{aligned}$$

从上面算出来的值可知，$P(C=c_2|x)>P(C=c_1|x)$，那么样本x被判断为c_2即不能被录取。朴素贝叶斯模型的举例也算是介绍了一下，但是我们上述条件概率中可以发现这么一个条件概率$P(F_2=f_{23}|C=c_2)=0$，那么当判断样本x属性值为$f_{11},f_{23},f_{31}$时，因为$P(F_2=f_{23}|C=c_2)=0$，那么连乘之后是等于0的，这显然有些不合理，所以有了[3.1 先验概率和属性的条件概率计算](#3.1 先验概率和属性的条件概率计算)中提到的拉普拉斯修正方法来进行修正。

4. 示例：使用朴素贝叶斯进行文本分类

以在线社区的留言板为例。为了不影响社区的发展，我们要屏蔽侮辱性的言论，所以要构建一个快速过滤器，如果某条留言使用了负面或者侮辱性的语言，那么就将该留言标识为内容不当。对此我们将言论分为两个类别：侮辱类和非侮辱类，分别用1和0表示。对于一般的文本处理，我们首先需要拆分文本，将文本拆分成一个个词条，词条其实可以想象成单词；之后将拆分之后的文本，表示成一个词条向量，1表示词条在文档中出现过，0表示词条未出现；之后基于这些向量来计算条件概率，并在此基础上构建朴素贝叶斯分类器。

4.1 获取词条列表和类别向量

这边我们暂时不涉及文本切分的操作，而是采用已经切分好的词条列表和类别向量，如下面代码所示

'''
:return
    postingList：文档被切分成一系列词条后的文档集合
    classVec：类别标签的集合，分为侮辱性和非侮辱性两类
'''
def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  # 1 代表侮辱性文字, 0 not
    return postingList, classVec

4.2 构建词向量

接下来我们需要创建词条向量，大致过程为：考虑出现在所有文档中的单词，构建词汇集合，词汇集合里面不包含相同的单词。之后将每篇文档转换为词汇表上的向量，文档中的单词若在词汇表中出现过一次，那么就在相应位置记作1，如果没有出现就在相应位置记作0。程序代码如下：

'''
创建文档集合的词汇表
:return 
    list(vocalSet):词汇表
'''
def createVocabList(docSet):
    vocabSet = set([])      # 词汇表Set集合
    for doc in docSet:      # 遍历得到词汇表Set集合
        vocabSet = vocabSet | set(doc)
    return list(vocabSet)


'''
把词条集合转换成词条向量
:return
    wordsVec:词条向量
'''
def wordsToVec(vocabList, inputWords):
    wordsVec = [0] * len(vocabList)
    for word in inputWords:
        if word in vocabList:
            wordsVec[vocabList.index(word)] = 1 # +=1 变成词袋模型
    return wordsVec

上述代码中createVocabList()函数会创建一个包含在文档中出现的不重复词的列表，即词汇表。获得词汇表之后，wordsToVec()函数则对输入的切分后的文本内容进行转化，转化为一个词条向量，向量中每一个元素为1或0，分别表示词汇表中的单词在输入的切分后的文本内容中是否出现，如果出现了则置为1。假如我们不以每个词的出现与否来设置向量的值，而是按照这个词出现的次数来设置向量的值，那么这种方式称为词袋模型，前者我们称为词集模型，词集模型中不能表达出一个词在文档中出现不止一次所包含的信息。下面是修改完之后的函数：

'''
把词条集合转换成词条向量，词袋模型
:return
    wordsVec:词条向量
'''
def wordsToVec(vocabList, inputWords):
    wordsVec = [0] * len(vocabList)
    for word in inputWords:
        if word in vocabList:
            wordsVec[vocabList.index(word)] += 1 
    return wordsVec

4.3 训练算法：从词向量计算概率

接下来使用得到的词条向量来计算概率。先采用未经过拉普拉斯修正的方式来计算概率，编写的代码如下：

'''
朴素贝叶斯的训练，即获取所需的条件概率;
暂时只支持二分类
'''
def trainNB0(dataTrain, classTrain):
    numTrainDoc = len(dataTrain)                    # 训练集的数量
    numWords = len(dataTrain[0])                    # 一条词向量的数量
    p1Train = np.sum(classTrain)/float(numTrainDoc)      # p1的概率
    p0Num = np.zeros(numWords)                       # 存放0类中各词汇数的array
    p1Num = np.zeros(numWords)                       # 存放1类中各词汇数的array
    p0Denom = 0.0                                   # 分母，0类中总词汇数
    p1Denom = 0.0                                   # 分母，1类中总词汇数
    for i in range(numTrainDoc):
        if classTrain[i] == 0:
            p0Num += dataTrain[i]
            p0Denom += np.sum(dataTrain[i])
        else:
            p1Num += dataTrain[i]
            p1Denom += np.sum(dataTrain[i])
    p0Vec = p0Num/p0Denom
    p1Vec = p1Num/p1Denom
    return p0Vec, p1Vec, p1Train

dataTrain是所有的词条向量组成的列表，classTrain是每篇文档类别标签所构成的向量，那么

np.sum(classTrain)/float(numTrainDoc)这个计算出来的就是p(1)的概率；

p0Num += dataTrain[i]这个操作主要对文档出现的单词进行计数，遍历之后最终得到的是类别为0下各单词数的情况；

p0Denom += np.sum(dataTrain[i])这个操作是对类别为0的文档的总单词进行计数；

p0Vec = p0Num/p0Denom这个公式是相当于计算条件概率了。

但是正如上文中有提到的那样，未经过拉普拉斯修正所得到的概率很有可能出现0，最后导致整个乘积为0，所以下面采用进行拉普拉斯修正后的方式，同时考虑到因为最终在概率连乘的情况会出现下溢出，就是很多很小的数相乘会出现下溢出或者得到不正确的答案。所以我们采用取自然对数的方式，将连乘的形式转化为了连加的形式可以有效避免下溢出或者浮点数舍入导致的错误，同时自然对数进行处理后不会有任何缺失。下面是最终修正后的代码

'''
朴素贝叶斯的训练，即获取所需的条件概率;
暂时只支持二分类
'''
def trainNB(dataTrain, classTrain):
    numTrainDoc = len(dataTrain)                    # 训练集的数量
    numWords = len(dataTrain[0])                    # 一条词向量的数量
    p1Train = np.sum(classTrain)/float(numTrainDoc)      # p1的概率
    p0Num = np.ones(numWords)                       # 存放0类中各词汇数的array
    p1Num = np.ones(numWords)                       # 存放1类中各词汇数的array
    p0Denom = 2.0                                   # 分母，0类中总词汇数
    p1Denom = 2.0                                   # 分母，1类中总词汇数
    for i in range(numTrainDoc):
        if classTrain[i] == 0:
            p0Num += dataTrain[i]
            p0Denom += np.sum(dataTrain[i])
        else:
            p1Num += dataTrain[i]
            p1Denom += np.sum(dataTrain[i])
    p0Vec = np.log(p0Num/p0Denom)
    p1Vec = np.log(p1Num/p1Denom)
    return p0Vec, p1Vec, p1Train

4.4 使用朴素贝叶斯模型进行分类

接下来我们需要编写对新样本进行分类的函数，实现的代码如下

'''
使用朴素贝叶斯进行决策
:input
    wordsVec:要分类的向量
'''
def classifyNB(wordsVec, p0Vec, p1Vec, p1Train):
    p0 = np.sum(wordsVec*p0Vec) + np.log(1-p1Train) # 获取属于0类的概率
    p1 = np.sum(wordsVec*p1Vec) + np.log(p1Train)   # 获取属于1类的概率
    if p0 < p1:
        return 1
    else:
        return 0

p0Vec, p1Vec, p1Train是训练得到的3个概率。即trainNB()函数返回的结果。

4.5 进行测试

最后我们编写测试代码来检验效果，编写的代码如下所示

def main():
    postList, postClasses = loadDataSet()   # 获取词条列表和类别向量
    vocalList = createVocabList(postList)   # 获取词汇表
    # 获取词汇向量
    trainWordsVecs = []
    for post in postList:
        trainWordsVecs.append(wordsToVec(vocalList, post))
    # 训练朴素贝叶斯
    p0Vec, p1Vec, p1Train = trainNB(np.array(trainWordsVecs), np.array(postClasses))
    # 测试
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = wordsToVec(vocalList, testEntry)
    print('%s 被分类为:%d'%(testEntry, classifyNB(np.array(thisDoc), p0Vec, p1Vec, p1Train)))
    testEntry = ['stupid', 'garbage']
    thisDoc = wordsToVec(vocalList, testEntry)
    print('%s 被分类为:%d' % (testEntry, classifyNB(np.array(thisDoc), p0Vec, p1Vec, p1Train)))

最终的输出结果如下所示：

['love', 'my', 'dalmation'] 被分类为:0
['stupid', 'garbage'] 被分类为:1

4.6 一点小疑惑

作者当初对最后计算条件概率的这个公式即 p0Vec = p0Num/p0Denom很不能理解，因为按照上文所述以及给出的例子来说，p0Num应该除以的是类别为0的样本总数，即应该除以的是len(classTrain)-np.sum(classTrain)，比如遍历完后的p0Num中，单词’my’显示出现了1次，那么根据上文所述，P（‘my’=1|0）应该为1/3，那为什么程序中要除以单词总数呢？作者个人认为，除以类别为0的样本总数这种方式中，我们更加偏向于把’my单词是否出现’当成了一个属性，而他的属性值为1或0。而书上的处理方式我们可以认为计算机的是P(‘my’|0)这个的概率，有点把单词的内容当成一个属性值，意思是在类别为0的文章中，‘my’这个单词出现的概率是多少，那么就是('my’出现的总次数/类别为0的总单词数)。当然从数学公式的角度，除以类别为0的总单词数和除以类别为0的样本，其实只是差了一个固定值。下面对这个方式编写相应的代码进行实验，其实主要修改trainNB()和classifyNB这两个函数即可：

'''
朴素贝叶斯的训练，即获取所需的条件概率;
暂时只支持二分类
'''
def trainNB(dataTrain, classTrain):
    numTrainDoc = len(dataTrain)  # 训练集的数量
    numWords = len(dataTrain[0])  # 一条词向量的数量
    p1Train = np.sum(classTrain) / float(numTrainDoc)  # p1的概率
    p0Num = np.ones(numWords)  # 存放0类中各单词出现的次数的array
    p1Num = np.ones(numWords)  # 存放1类中各单词出现的次数的array
    p0Denom = len(classTrain) - np.sum(classTrain) + 2  # 分母，0类中总词汇数
    p1Denom = np.sum(classTrain) + 2  # 分母，1类中总词汇数
    for i in range(numTrainDoc):
        if classTrain[i] == 0:
            p0Num += dataTrain[i]
        else:
            p1Num += dataTrain[i]
    p01Vec = np.log(p0Num / p0Denom)
    p11Vec = np.log(p1Num / p1Denom)
    return p01Vec, p11Vec, p1Train


'''
使用朴素贝叶斯进行决策
'''
def classifyNB(wordsVec, p01Vec, p11Vec, p1Train):
    p00Vec = 1 - p01Vec # 类别为0的文档中，各词汇未出现的条件概率
    p10Vec = 1 - p11Vec # 类别为1的文档中，各词汇未出现的条件概率
    wordsVecT = 1 - wordsVec    # 向量进行转化，未出现的词汇变为1
    # 分别计算属于0类或者1类的概率
    p0 = np.sum(wordsVec * p01Vec + wordsVecT * p00Vec) + np.log(1 - p1Train)
    p1 = np.sum(wordsVec * p11Vec + wordsVecT * p10Vec) + np.log(p1Train))
    if p0 < p1:
        return 1
    else:
        return 0

主要修改内容是trainNB()函数中的分母

p0Denom = len(classTrain) - np.sum(classTrain) + 2  # 分母，0类中总词汇数
p1Denom = np.sum(classTrain) + 2  # 分母，1类中总词汇数

以及classifyNB()函数中对最终所属类别概率的计算

p00Vec = 1 - p01Vec # 类别为0的文档中，各词汇未出现的条件概率
p10Vec = 1 - p11Vec # 类别为1的文档中，各词汇未出现的条件概率
wordsVecT = 1 - wordsVec    # 向量进行转化，未出现的词汇变为1
# 分别计算属于0类或者1类的概率
p0 = np.sum(wordsVec * p01Vec + wordsVecT * p00Vec) + np.log(1 - p1Train)
p1 = np.sum(wordsVec * p11Vec + wordsVecT * p10Vec) + np.log(p1Train)

最后对这种方式进行测试，输出的结果同上：

['love', 'my', 'dalmation'] 被分类为:0
['stupid', 'garbage'] 被分类为:1

5. 实战：使用朴素贝叶斯过滤垃圾邮件

上面的例子使我们对朴素贝叶斯的应用有了一定的认识，下面我们再来一个实战，加深对朴素贝叶斯和文本处理的印象。我们希望通过这个实战，来对朴素分类器的效果进行判断，实战中使用错误率来展示效果。首先需要对文本进行切分，将其解析成词条—>分成训练集和测试集—>将解析之后的内容转化为词条向量—>训练朴素贝叶斯模型—>在测试集上进行测试给出错误率。

5.1 准备数据：切分文本

如我们要对下面这文本进行切分，

Hi Peter,

With Jose out of town, do you want to
meet once in a while to keep things
going and do some interesting stuff?

Let me know
Eugene

那么可以使用正则表达式来对其进行切分，编写相应的代码如下：

'''
将读取的内容进行解析，返回文档解析后的词条列表
'''
def textParse(bigString):
    listOfTokens = re.split("\W*", bigString)
    return [token.lower() for token in listOfTokens if len(token) > 2]

其中bigString是文件读取到的内容，我们使用正则表达式对其进行切分，使用的\W*表示分隔符是除字母、数字、下划线的字符。在返回的列表中，我们全都将单词转化为小写，并且单词的长度至少为3。转化为小写，是我们希望所有词的形式都是统一的，而长度要大于2，是因为在分隔URL中可能出现en或py等情况，如answer.py?hl=en&answer=174623，我们想去掉这些单词。下面配合上文件内容读取和对文本信息的切分的代码后，我们就可以将所有的文档数据集转化为词条了：

'''
读取文本内容    
'''
def loadDateSet():
    docList = []    # 所有文档解析后的词条集合
    classList = []  # 文档对应的类别，spam为1，ham为0

    for i in range(1, 26):
        with open("email/spam/%d.txt"%i) as f:
            wordsList = textParse(f.read())
            docList.append(wordsList)
            classList.append(1)
        with open("email/ham/%d.txt"%i) as f:
            wordsList = textParse(f.read())
            docList.append(wordsList)
            classList.append(0)
    return docList, classList

上述代码将数据集全都解析成了词列表，同时对来自spam目录的文本附上了类别1，对来自ham目录的文本附上了类别0。

5.2 构建训练集和测试集

实战中一共有50封电子邮件，不是很多，随机选择其中10封作为测试集。

'''
训练集和测试集分开
'''
def testTrainSplit(docList):
    trainListIndex = list(range(len(docList)))
    testListIndex= []

    for i in range(10):
        randIndex = int(np.random.uniform(0, len(trainListIndex)))
        testListIndex.append(trainListIndex[randIndex])
        del(trainListIndex[randIndex])
    return trainListIndex, testListIndex

上面并没有将真正的数据集进行了切分，而是随机产生了总数据集中需作为测试集的索引列表。

5.3 转化为词条向量

这块的代码同本篇中言论过滤器那个例子一样，所以不再赘述。

5.4 在训练集上进行训练，获得所需概率值

这块的代码同本篇中言论过滤器那个例子一样，所以不再赘述。

5.5 使用朴素贝叶斯模型进行分类

这块的代码同本篇中言论过滤器那个例子一样，所以不再赘述。

5.6 编写整个程序执行流程，计算错误率

整个程序执行的代码如下所示，我们进行了10次实验，并计算平均错误率，编写的代码如下：

def main():
    docList, classList = loadDateSet()  # 文档总的词条列表，类别列表
    vocabList = createVocabList(docList)  # 文档的词汇集

    sumErrorRate = 0.0  # 总的错误率
    for k in range(10):
        trainListIndex, testListIndex = testTrainSplit(docList)  # 训练集、测试集的index
        # 获取训练集词条向量
        trainWordVecs = []  # 训练集词向量
        trainClass = []  # 训练集词向量类别
        for i in trainListIndex:
            trainWordVecs.append(wordsToVec(vocabList, docList[i]))
            trainClass.append(classList[i])

        # 训练，获取所需概率值
        spam1Vec, ham1Vec, pSpamTrain = trainNB(np.array(trainWordVecs),
                                                np.array(trainClass))

        errorCount = 0  # 测试集上的错误次数
        for docIndex in testListIndex:
            wordVec = wordsToVec(vocabList, docList[docIndex])
            if classList[docIndex] != int(classifyNB(
                    np.array(wordVec), spam1Vec, ham1Vec, pSpamTrain)):
                errorCount += 1
                print("第%d次实验中，错分的词列表为：%s"%(k, docList[docIndex]))
        sumErrorRate += errorCount / len(testListIndex)
        print("第%d次实验中，在测试集上的错误率为%f" % (k, errorCount / len(testListIndex)))
    print("在10次实验过程中，测试集上的平均错误率为%f"%(sumErrorRate/float(10)))

最终的输出结果如下，10次实验的平均错误率为6%左右

第0次实验中，错分的词列表为：['yeah', 'ready', 'may', 'not', 'here', 'because', 'jar', 'jar', 'has', 'plane', 'tickets', 'germany', 'for']
第0次实验中，在测试集上的错误率为0.100000
第1次实验中，在测试集上的错误率为0.000000
第2次实验中，在测试集上的错误率为0.000000
第3次实验中，错分的词列表为：['benoit', 'mandelbrot', '1924', '2010', 'benoit', 'mandelbrot', '1924', '2010', 'wilmott', 'team', 'benoit', 'mandelbrot', 'the', 'mathematician', 'the', 'father', 'fractal', 'mathematics', 'and', 'advocate', 'more', 'sophisticated', 'modelling', 'quantitative', 'finance', 'died', '14th', 'october', '2010', 'aged', 'wilmott', 'magazine', 'has', 'often', 'featured', 'mandelbrot', 'his', 'ideas', 'and', 'the', 'work', 'others', 'inspired', 'his', 'fundamental', 'insights', 'you', 'must', 'logged', 'view', 'these', 'articles', 'from', 'past', 'issues', 'wilmott', 'magazine']
第3次实验中，在测试集上的错误率为0.100000
第4次实验中，错分的词列表为：['home', 'based', 'business', 'opportunity', 'knocking', 'your', 'door', 'don抰', 'rude', 'and', 'let', 'this', 'chance', 'you', 'can', 'earn', 'great', 'income', 'and', 'find', 'your', 'financial', 'life', 'transformed', 'learn', 'more', 'here', 'your', 'success', 'work', 'from', 'home', 'finder', 'experts']
第4次实验中，在测试集上的错误率为0.100000
第5次实验中，在测试集上的错误率为0.000000
第6次实验中，在测试集上的错误率为0.000000
第7次实验中，错分的词列表为：['yeah', 'ready', 'may', 'not', 'here', 'because', 'jar', 'jar', 'has', 'plane', 'tickets', 'germany', 'for']
第7次实验中，在测试集上的错误率为0.100000
第8次实验中，错分的词列表为：['yeah', 'ready', 'may', 'not', 'here', 'because', 'jar', 'jar', 'has', 'plane', 'tickets', 'germany', 'for']
第8次实验中，在测试集上的错误率为0.100000
第9次实验中，错分的词列表为：['home', 'based', 'business', 'opportunity', 'knocking', 'your', 'door', 'don抰', 'rude', 'and', 'let', 'this', 'chance', 'you', 'can', 'earn', 'great', 'income', 'and', 'find', 'your', 'financial', 'life', 'transformed', 'learn', 'more', 'here', 'your', 'success', 'work', 'from', 'home', 'finder', 'experts']
第9次实验中，在测试集上的错误率为0.100000
在10次实验过程中，测试集上的平均错误率为0.060000

5.6 额外的实验

对于言论分类中的疑惑，再次在这个实战中将其按照疑惑中的另一种方法进行修改，修改的还是trainNB()和classifyNB()这两个函数，修改后的代码如下：

'''
朴素贝叶斯的训练
'''
def trainNB(trainMat, trainClass):
    numTrainDoc = len(trainMat)
    numWords = len(trainMat[0])
    pSpam = np.sum(trainClass) / float(numTrainDoc)
    spamNum = np.ones(numWords)
    hamNum = np.ones(numWords)
    spamDenom = np.sum(trainClass) + 2
    hamDenom = len(trainClass) - np.sum(trainClass) + 2
    for i in range(numTrainDoc):
        if trainClass[i] == 1:
            spamNum += trainMat[i]
        else:
            hamNum += trainMat[i]
    spam1Vec = np.log(spamNum / spamDenom)
    ham1Vec = np.log(hamNum / hamDenom)
    return spam1Vec, ham1Vec, pSpam

'''
朴素贝叶斯进行决策
'''
def classifyNB(inputDoc, spam1Vec, ham1Vec, pSpamTrain):
    pSpam = 0.0
    pHam = 0.0
    for i in range(len(inputDoc)):
        if inputDoc[i] == 1:
            pSpam += spam1Vec[i]
            pHam += ham1Vec[i]
        else:
            pSpam += (1 - spam1Vec[i])
            pHam += (1 - ham1Vec[i])
    pSpam += np.log(pSpamTrain)
    pHam += np.log(1 - pSpamTrain)
    if pSpam > pHam:
        return 1
    else:
        return 0

同样对其进行了10次实验，发现10次实验的平均错误率有点高

在10次实验过程中，测试集上的平均错误率为0.510000

所以我们在下次的实验中还是采用书上所说的那种方法对其进行计算概率较好。

6. 总结

• 朴素贝叶斯对小规模的数据表现很好，适合多分类任务，适合增量式训练，算法也比较简单。
• 由于朴素贝叶斯的“朴素”特点，所以会带来一些准确率上的损失。
• 对输入数据的表达形式很敏感。
• 朴素贝叶斯的准确率，其实是比较依赖于训练语料的，机器学习算法就和纯洁的小孩一样，取决于其成长（训练）条件，“吃的是草挤的是奶”，但"不是所有的牛奶，都叫特仑苏"。

附：代码和数据集链接

本文中所有的代码和使用到的数据集均可在https://github.com/DawnGuoDev/MachineLearningStudy/tree/master/NaiveBayes中找到哦。

本文参考及推荐

1. 周志华，机器学习
2. Peter Harrington，机器学习实战
3. Gitchat，21天入门机器学习-第02期